【题目】透明的口袋里装有3个球,这3个球分别标有数字1、2、3,这些球除了数字外都相同。
(1)如果从袋中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?(3分)
(2)小明和小东玩摸球游戏,游戏规则如下:先由小明随机摸出一个球,记下球的数字后放回,搅匀后再由小东随机摸出一个球,记下球的数字.谁摸出的球的数字大,谁获胜.现请你利用树状图或列表的方法分析游戏规则对双方是否公平?并说明理由。(6分)
参考答案:
【答案】(1)![]() .(2)公平,理由见解析.
.(2)公平,理由见解析.
【解析】试题分析:(1)利用概率公式直接求出即可;
(2)首先利用列表法求出两人的获胜概率,判断双方取胜所包含的情况数目是否相等,即可得出答案.
试题解析:(1)从3个球中随机摸出一个,摸到标有数字是2的球的概率是:![]() .
.
(2)游戏规则对双方公平.列表如下:
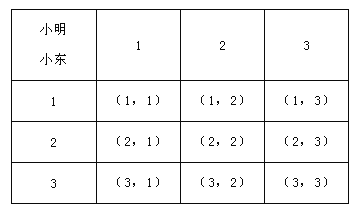
由表可知,P(小明获胜)=![]() ,P(小东获胜)=
,P(小东获胜)=![]() ,
,
∵P(小明获胜)=P(小东获胜),
∴游戏规则对双方公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国的茶文化源远流长,根据制作方法和茶多酚氧化(发酵)程度的不同,可分为六大类:绿茶(不发酵)、白茶(轻微发酵)、黄茶(轻发酵)、青茶(半发酵)、黑茶(后发酵)、红茶(全发酵).春节将至,为款待亲朋好友,小叶去茶庄选购茶叶.茶庄有碧螺春、龙井两种绿茶,一种青茶——武夷岩茶及一种黄茶——银针出售.
(1)随机购买一种茶叶,是绿茶的概率为________;
(2)随机购买两种茶叶,求一种是绿茶、一种是银针的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为坐标原点,四边形ABCD是菱形,A(-4,4),B点在第一象限,AB=5,AB与y轴交于点F,对角线AC交y轴于点E.
(1)直接写出B点C点坐标;
(2)动点P从C点出发以每秒1个单位的速度沿折线段C—D—A运动,求△EDP的面积y与时间t的关系式
(3)在(2)的条件下,是否存在一点P,使△APE沿其一边翻折构成的四边形是菱形,若存在,求出点P坐标;若不存在,请说明理由.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲、乙两人在一次射击比赛中击中靶的情况(击中靶中心“×”所在的圆面为10环,靶中各数字表示该数所在圆环被击中所得的环数),每人射击了6次.
(1)请用列表法将他俩的射击成绩统计出来;
(2)请你运用所学的统计知识做出分析,从两个不同角度评价甲、乙两人的打靶成绩.

-
科目: 来源: 题型:
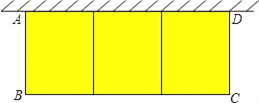
查看答案和解析>>【题目】如图,在一面靠墙的空地上用长为24米的篱笆,围成中间隔有二道篱笆的长方形花圃,设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式及自变量的取值范围;
(2)当x取何值时所围成的花圃面积最大,最大值是多少?
(3)若墙的最大可用长度为8米,则求围成花圃的最大面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两根木条,一根长20cm,另一根长24cm,将它们一端重合且放在同一条直线上,此时两根木条的中点之间的距离为( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场在“双十一”促销活动中决定对购买空调的顾客实行现金返利.规定每购买一台空调,商场返利若干元.经调查,销售空调数量y1(单位:台)与返利x(单位:元)之间的函数表达式为
 .每台空调的利润y2(单位:元)与返利x的函数图像如图所示.
.每台空调的利润y2(单位:元)与返利x的函数图像如图所示.(1)求y2与x之间的函数表达式;

(2)每台空调返利多少元才能使销售空调的总利润最大?最大总利润是多少?
相关试题

