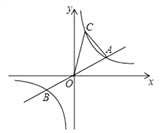
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式
交于A、B两点,A点的横坐标为3,则下列结论:①k=3;②关于x的不等式![]() 的解集为
的解集为![]() 或
或![]() ;③若双曲线
;③若双曲线![]() 上有一点C的纵坐标为6,则△AOC的面积为8;④若在
上有一点C的纵坐标为6,则△AOC的面积为8;④若在![]() 轴上有一点M,
轴上有一点M,![]() 轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
轴上有一点N,且点M、N、A、C四点恰好构成平行四边形,则M、N点的坐标分别为M(2,0)、N(0,4),其中正确结论的个数( )
A. 4个 B. 3个 C. 2个 D. 1个
参考答案:
【答案】B
【解析】分析:①直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为3,代入正比例函数,可求得点A的坐标,继而求得k值;②根据对称性,可求得点B的坐标,结合图象,即可求得关于x的不等式
交于A、B两点,A点横坐标为3,代入正比例函数,可求得点A的坐标,继而求得k值;②根据对称性,可求得点B的坐标,结合图象,即可求得关于x的不等式![]() 的解集;③过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC=S△OCD+S梯形AEDC-S△AOE=S梯形AEDC,又由双曲线y=
的解集;③过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,可得S△AOC=S△OCD+S梯形AEDC-S△AOE=S梯形AEDC,又由双曲线y=![]() (k>0)上有一点C的纵坐标为6,即可求得点C的坐标,继而求得答案;④由当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,根据平移的性质,即可求得答案.
(k>0)上有一点C的纵坐标为6,即可求得点C的坐标,继而求得答案;④由当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,根据平移的性质,即可求得答案.
详解:
∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,A点横坐标为3,
交于A、B两点,A点横坐标为3,
∴点A的纵坐标为:y=![]() ×3=2,
×3=2,
∴点A(3,2),
∴2=![]() ,
,
∴k=6;
①错误;
∵直线![]() 与双曲线
与双曲线![]() 交于A、B两点,点A(3,2),
交于A、B两点,点A(3,2),
∴B(-3,-2),
∴关于x的不等式![]() 的解集为
的解集为![]() 或
或![]() ;
;
②正确;
过点C作CD⊥x轴于点D,过点A作AE⊥轴于点E,
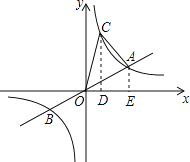
∵双曲线y=![]() (k>0)上有一点C的纵坐标为6,
(k>0)上有一点C的纵坐标为6,
∴把y=6代入y=![]() 得:x=1,
得:x=1,
∴点C(1,6),
∴S△AOC=S△OCD+S梯形AEDC-S△AOE=S梯形AEDC=![]() ×(2+6)×(3-1)=8;
×(2+6)×(3-1)=8;
③正确;
如图,当MN∥AC,且MN=AC时,点M、N、A、C四点恰好构成平行四边形,
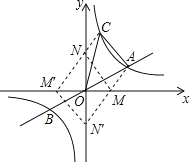
∵点A(3,2),点C(1,6),
∴根据平移的性质可得:M(2,0),N(0,4)或M′(-2,0),N′(0,-4).
④正确;
综上,正确的结论有3个,故选B.
-
科目: 来源: 题型:
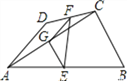
查看答案和解析>>【题目】如图,四边形 ABCD 中,AD=BC,E、F、G 分别是 AB、CD、AC 的中点,若∠DAC=20 ,∠ACB=90 ,则 ∠FEG=( )
A.
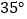 B.
B. 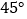 C.
C. 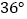 D.
D. 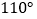
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,∠B=60°.G是CD的中点,E是边AD上的动点,EG的延长线与BC的延长线交于点F,连结CE,DF,下列说法不正确的是( )
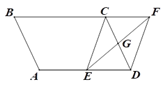
A. 四边形CEDF是平行四边形
B. 当
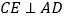 时,四边形CEDF是矩形
时,四边形CEDF是矩形C. 当
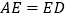 时,四边形CEDF是菱形
时,四边形CEDF是菱形D. 当
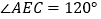 时,四边形CEDF是菱形
时,四边形CEDF是菱形 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD的边长为12,E是BC中点,将正方形边CD沿DE折叠到DF,将AD折叠,使AD与DF重合,折痕交AB于G,连接BF,CF,则下列结论:①G、F、E三点共线;②BG=8;③△BEF∽△CDF;④S△BFG=
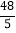 .其中正确的有( )
.其中正确的有( )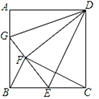
A. ①② B. ①②③ C. ②③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,M,N分别为BC,CD的中点,AM=1,AN=2,∠MAN=60°,AM ,DC的延长线相交于点E,则AB的长为_____________;
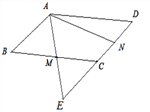
-
科目: 来源: 题型:
查看答案和解析>>【题目】目前“微信”、“支付宝”、“共享单车”和“网购”给我们带来了很多便利,初二数学小组在校内对“你最认可的四大新生事物”进行了调查,随机调查了
 人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
人(每名学生必选一种且只能从这四种中选择一种)并将调查结果绘制成如下不完整的统计图.
(1)根据图中信息求出
 =___________,
=___________, =_____________;
=_____________;(2)请你帮助他们将这两个统计图补全;
(3)根据抽样调查的结果,请估算全校2000名学生种,大约有多少人最认可“微信”这一新生事物?
-
科目: 来源: 题型:
查看答案和解析>>【题目】现有甲、乙两个体育用品商店出售乒乓球拍和乒乓球,球拍每块价格为48元,乒乓球每个价格为2元,已知甲店制定的优惠方法是买--块球拍送6个乒乓球,乙店按总价的
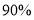 收费,某球队需要购买球拍4块,乒乓球
收费,某球队需要购买球拍4块,乒乓球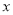 个(不少于24个).
个(不少于24个).(1)试用含有的代数式表示甲、乙两店购买球拍4块,乒乓球
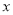 个的费用.
个的费用.(2)当需要购买240个乒乓球时,选择哪家商店购买更优惠?请说明理由.
(3)当购买多少个乒乓球时,两个商店的收费一样多?
相关试题

