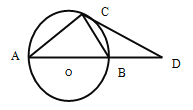
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
参考答案:
【答案】 AB=2BC CD是切线 ∠BCD=∠D=30°
【解析】解:∵AB是⊙O的直径,BD=OB,∴∠ACB=90°.
又∵∠CAB=30°,∴AB=2BC.
连接OC,BC.∵AB是⊙O的直径,∴∠ACB=90°.∵∠CAB=30°,∴∠COB=∠CBO=60°,∴△OBC是等边三角形.∵BD=OB,∴BD=OB=BC=OC,∴∠D=∠BCD=![]() ∠CBO=30°,∴∠A=∠D,∠OCD=90°,即OC⊥CD,∴AC=DC,CD是⊙O的切线,∴∠D=∠BCD=30°.
∠CBO=30°,∴∠A=∠D,∠OCD=90°,即OC⊥CD,∴AC=DC,CD是⊙O的切线,∴∠D=∠BCD=30°.
故答案为:此题答案不唯一,如AB=2BC,CD是切线,∠BCD=∠D=30°等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,点
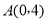 在
在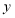 轴上,点
轴上,点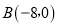 在
在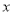 轴上.
轴上.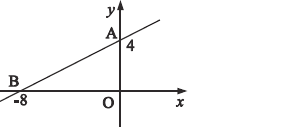
(1)求直线
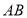 的解析式;
的解析式;(2)若
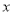 轴上有一点
轴上有一点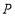 使得
使得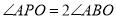 时,求
时,求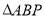 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为__度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学完三角形的高后,小明对三角形与高线做了如下研究:如图,
 是
是 中边
中边 上的-点,过点
上的-点,过点 、
、 分别作、
分别作、 、
、 、
、 ,垂足分别为点
,垂足分别为点 、
、 、
、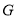 ,由
,由 与
与 的面积之和等于
的面积之和等于 的面积,有等量关系式:
的面积,有等量关系式: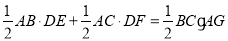 .像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.
.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.


图(1) 图(2)
(1)如图(1), 矩形
 中,
中, ,
, ,点
,点 是
是 上一点,过点
上一点,过点 作
作 ,
, ,垂足分别为点
,垂足分别为点 、
、 ,求
,求 的值;
的值;(2)如图(2),在
 中,角平分线
中,角平分线 、
、 相交于点
相交于点 ,过点
,过点 分别作
分别作 、
、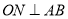 ,垂足分别为点
,垂足分别为点 、
、 ,若
,若 ,
, ,求四边形
,求四边形 的周长.
的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形.请你参考这个作全等三角形的方法,解答下列问题:
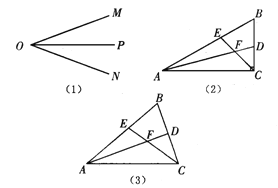
(1)如图(2),在△ABC中,∠ACB是直角,∠B=60°, AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你判断并写出FE与FD之间的数量关系;
(2)如图(3),在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(1)中所得结论是否仍然成立?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的图象如图,给出下列四个结论:①abc>0;②4ac﹣b2<0;③4a+c<2b;④3b+2c<0;⑤m(am+b)+b<a(m≠﹣1).其中结论正确的个数是( )
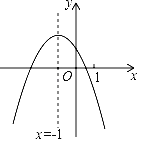
A. 2 B. 3 C. 4 D. 5
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的盒子中放有四张分别写有数字1、2、3、4的红色卡片和三张分别写有数字1、2、3的蓝色卡片,卡片除颜色和数字外完全相同.
(1)从中任意抽取一张卡片,求该卡片上写有数字2的概率;
(2)将三张蓝色卡片取出后放入另外一个不透明的盒子内,然后在两个盒子内各任意抽取一张卡片,以红色卡片上的数字作为十位数,蓝色卡片上的数字作为个位数组成个两位数,求这个两位数大于30的概率.
相关试题

