【题目】如图,平面直角坐标系中,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上.
轴上.
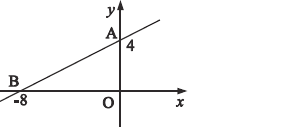
(1)求直线![]() 的解析式;
的解析式;
(2)若![]() 轴上有一点
轴上有一点![]() 使得
使得![]() 时,求
时,求![]() 的面积.
的面积.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() 的面积为
的面积为![]() 或
或![]()
【解析】
(1)根据点A,B的坐标,利用待定系数法可求出直线AB的解析式;
(2)设点P的坐标为(t,0),分点P在原点左侧及点P在原点右侧两种情况考虑:①若点P在x轴上原点左侧,当PB=AP时,∠APO=2∠ABO,在Rt△APO中,利用勾股定理可求出t的值,进而可得出BP的长,再利用三角形的面积公式可求出△ABP的面积;②若点P在x轴上原点右侧,由对称性,可得出点P′的坐标,进而可得出BP′的长,再利用三角形的面积公式可求出△ABP′的面积.综上,此题得解
解:(1)设直线![]() 的解析式为
的解析式为![]() ,则:
,则:
![]() 解得:
解得:![]()
∴所求直线![]() 的解析式为:
的解析式为: ![]()
(2)设点![]() 为
为![]()
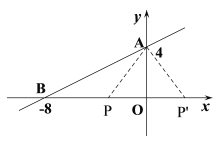
①若点![]() 在
在![]() 轴上原点左侧,当
轴上原点左侧,当![]() 时,
时,![]()
在![]() 中,
中,![]() ,
,![]() ,
,![]()
∴ ![]()
解得: ![]()
∴![]()
∴![]()
②若![]() 点在
点在![]() 轴上原点右侧,由对称性,得
轴上原点右侧,由对称性,得![]() 点为
点为![]() ,此时
,此时![]() ,
,
∴![]()
综合上述,![]() 的面积为
的面积为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有公共端点
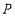 的两条线段
的两条线段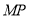 ,
,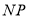 组成一条折线
组成一条折线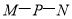 ,若该折线
,若该折线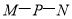 上一点
上一点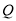 把这条折线分成相等的两部分,我们把这个点
把这条折线分成相等的两部分,我们把这个点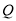 叫做这条折线的“折中点”.已知点
叫做这条折线的“折中点”.已知点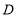 是折线
是折线 的“折中点”,点
的“折中点”,点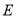 为线段
为线段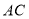 的中点,
的中点,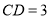 ,
,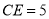 ,则线段
,则线段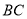 的长为______.
的长为______.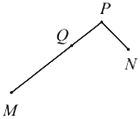
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划购进一批自行车. 男式自行车价格为
 元/辆,女式自行车价格为
元/辆,女式自行车价格为 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多 辆,设购进女式自行车
辆,设购进女式自行车 辆,购置总费用为
辆,购置总费用为 元.
元.(1)求购置总费用
 (元)与女式单车
(元)与女式单车 (辆)之间的函数关系式;
(辆)之间的函数关系式;(2)若两种自行车至少需要购置
 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,货轮
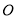 在航行过程中,发现灯塔
在航行过程中,发现灯塔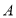 在它的南偏东
在它的南偏东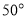 方向上.同时,在它的北偏东
方向上.同时,在它的北偏东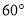 、西北(西偏北
、西北(西偏北 )方向上又分别发现了客轮
)方向上又分别发现了客轮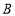 和海岛
和海岛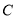 .
.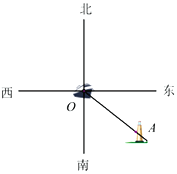
(1)仿照表示灯塔方位的方法,分别画出客轮
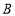 和海岛
和海岛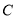 方向的射线;
方向的射线;(2)另一货轮
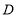 在平面内所组成的
在平面内所组成的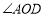 与
与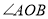 互为补角,请画出货轮
互为补角,请画出货轮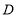 方向的射线并写出所在的方位角.
方向的射线并写出所在的方位角. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABE和△ADC是△ABC分别沿着AB、AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为__度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】学完三角形的高后,小明对三角形与高线做了如下研究:如图,
 是
是 中边
中边 上的-点,过点
上的-点,过点 、
、 分别作、
分别作、 、
、 、
、 ,垂足分别为点
,垂足分别为点 、
、 、
、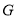 ,由
,由 与
与 的面积之和等于
的面积之和等于 的面积,有等量关系式:
的面积,有等量关系式: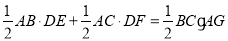 .像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.
.像这种利用同一平面图形的两种面积计算途径可以得出相关线段的数量关系式,从而用于解决数学问题的方法称为“等积法”,下面请尝试用这种方法解决下列问题.


图(1) 图(2)
(1)如图(1), 矩形
 中,
中, ,
, ,点
,点 是
是 上一点,过点
上一点,过点 作
作 ,
, ,垂足分别为点
,垂足分别为点 、
、 ,求
,求 的值;
的值;(2)如图(2),在
 中,角平分线
中,角平分线 、
、 相交于点
相交于点 ,过点
,过点 分别作
分别作 、
、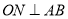 ,垂足分别为点
,垂足分别为点 、
、 ,若
,若 ,
, ,求四边形
,求四边形 的周长.
的周长. -
科目: 来源: 题型:
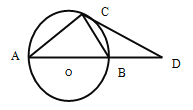
查看答案和解析>>【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
相关试题

