【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )

A. ![]() +1B. 2
+1B. 2![]() ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣![]()
参考答案:
【答案】A
【解析】
连接PD,依据SAS构造全等三角形,即△BCE≌△DCP,将BE的长转化为PD的长,再依据垂线段最短得到当DP最短时,BE亦最短,根据∠O=30°,OD=2+2![]() ,即可求得DP的长的最小值.
,即可求得DP的长的最小值.
解:如图,连接PD,
由题意可得,PC=EC,∠PCE=90°=∠DCB,BC=DC,
∴∠DCP=∠BCE,
在△DCP和△BCE中,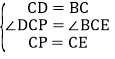 ,
,
∴△DCP≌△BCE(SAS),
∴PD=BE,
当DP⊥OM时,DP最短,此时BE最短,
∵∠AOB=30°,AB=2=AD,
∴OD=OA+AD=2![]() +2,
+2,
∴当DP⊥OM时,DP=![]() OD=
OD=![]() +1,
+1,
∴BE的最小值为![]() +1.
+1.
故选:A.
-
科目: 来源: 题型:
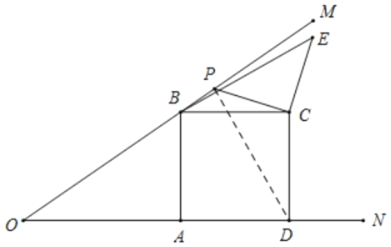
查看答案和解析>>【题目】如图,
 为
为 轴正半轴上一动点,
轴正半轴上一动点,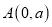 ,
, ,且
,且 、
、 满足
满足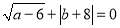 ,
, .
.
(1)求
 的面积;
的面积;(2)若
 ,
, 、
、 为线段
为线段 上的动点,作
上的动点,作 交
交 于
于 ,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB=
,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB= ,求∠BAC(用
,求∠BAC(用 表示);
表示);(3)若
 ,
, 轴于
轴于 ,点
,点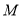 从
从 点出发,在射线
点出发,在射线 上运动,同时另一动点
上运动,同时另一动点 从点
从点 向
向 点运动,到
点运动,到 停止运动,
停止运动,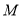 、
、 的速度分别为2个单位/秒、3个单位/秒,当
的速度分别为2个单位/秒、3个单位/秒,当 时,求运动的时间.
时,求运动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )
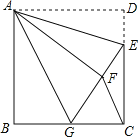
A. 1B. 2C. 3D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣
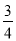 x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求
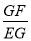 的值.
的值.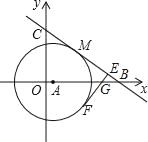
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为a厘米,宽为b厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
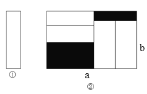
A. 4a厘米B. 4b厘米C. 2(a+b)厘米D. 4(a-b)厘米
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
与x轴交于A(-1,0)和B(3,0)两点,与y轴交于点C,对称轴与x轴交于点E,点D为顶点,连接BD、CD、BC.
(1)求证△BCD是直角三角形;
(2)点P为线段BD上一点,若∠PCO+∠CDB=180°,求点P的坐标;
(3)点M为抛物线上一点,作MN⊥CD,交直线CD于点N,若∠CMN=∠BDE,请直接写出所有符合条件的点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为弘扬“雷锋精神”,我县开展“做雷锋精神种子.当四品八德少年”主题征文比赛,已知每篇参赛征文成绩记
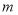 分(
分(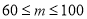 ) ,组委会从
) ,组委会从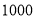 篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.
篇征文中随机抽取了部分参赛征文,统计了它们的成绩,并绘制了如图不完整的两幅统计图表.县主题征文比赛成绩频数分布表
分数段
频数
频率
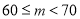
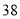

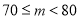
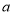
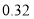

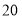
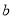
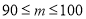
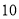
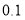
合计
县主题征文比赛成绩频数分布直方图
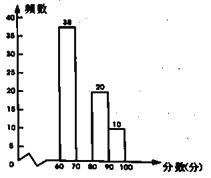
请根据以上信息,解决下列问题:
(1)征文比赛成绩频数分布表中
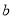 的值是 ;
的值是 ;(2)补全征文比赛成绩频数分布直方图:
(3)若
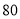 分以上(含
分以上(含 分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
分)的征文将被评为一等奖,请估算全县获得一等奖征文的篇数.
相关试题

