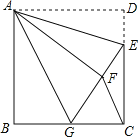
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;② BG=GC;③ AG∥CF;④∠GAE=45°.
则正确结论的个数有( )
A. 1B. 2C. 3D. 4
参考答案:
【答案】D
【解析】
根据正方形的性质得出AB=AD=DC=6,∠B=D=90°,求出DE=2,AF=AB,根据HL推出Rt△ABG≌Rt△AFG,推出BG=FG,∠AGB=∠AGF,设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2,在Rt△ECG中,由勾股定理得出(6-x)2+42=(x+2)2,求出x=3,得出BG=GF=CG,求出∠AGB=∠FCG,推出AG∥CF,根据全等得出∠DAE=∠FAE,∠BAG=∠FAG.
解:∵四边形ABCD是正方形,
∴AB=AD=DC=6,∠B=D=90°,
∵CD=3DE,
∴DE=2,
∵△ADE沿AE折叠得到△AFE,
∴DE=EF=2,AD=AF,∠D=∠AFE=∠AFG=90°,
∴AF=AB,
∵在Rt△ABG和Rt△AFG中
![]() ,
,
∴Rt△ABG≌Rt△AFG(HL).
∴①正确;
∵Rt△ABG≌Rt△AFG,
∴BG=FG,∠AGB=∠AGF.
设BG=x,则CG=BC-BG=6-x,GE=GF+EF=BG+DE=x+2.在Rt△ECG中,由勾股定理得:CG2+CE2=EG2.
∵CG=6-x,CE=4,EG=x+2,
∴(6-x)2+42=(x+2)2,解得:x=3.
∴BG=GF=CG=3.
∴②正确;
∵CG=GF,
∴∠CFG=∠FCG.
∵∠BGF=∠CFG+∠FCG,∠BGF=∠AGB+∠AGF,
∴∠CFG+∠FCG=∠AGB+∠AGF.
∵∠AGB=∠AGF,∠CFG=∠FCG,
∴∠AGB=∠FCG.
∴AG∥CF.
∴③正确;
∵△ADE沿AE折叠得到△AFE,
∴△DAE≌△FAE.
∴∠DAE=∠FAE.
∵△ABG≌△AFG,
∴∠BAG=∠FAG.
∵∠BAD=90°,
∴∠EAG=∠EAF+∠GAF=![]() ×90°=45°.
×90°=45°.
∴④正确.
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,点A1,A2,A3,A4和C1,C2,C3,C4分别是ABCD的五等分点,点B1,B2和D1,D2分别是BC和DA的三等分点,已知四边形A4B2C4D2的面积为2,则平行四边形ABCD的面积为( )

A. 4 B.
 C.
C.  D. 30
D. 30 -
科目: 来源: 题型:
查看答案和解析>>【题目】某文具店购进
 、
、 两种文具进行销售.若每个
两种文具进行销售.若每个 种文具的进价比每个
种文具的进价比每个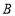 种文具的进价少2元,且用900元正好可以购进50个
种文具的进价少2元,且用900元正好可以购进50个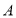 种文具和50个
种文具和50个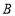 种文具,
种文具,(1)求每个
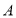 种文具和
种文具和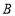 种文具的进价分别为多少元?
种文具的进价分别为多少元?(2)若该文具店购进
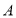 种文具的数量比购进
种文具的数量比购进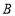 种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个
种文具的数量的3倍还少5个,购进两种文具的总数量不超过95个,每个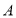 种文具的销售价格为12元,每个
种文具的销售价格为12元,每个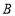 种文具的销售价格为15元,则将购进的
种文具的销售价格为15元,则将购进的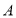 、
、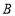 两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进
两种文具全部售出后,可使总利润超过371元,通过计算求出该文具店购进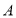 、
、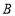 两种文具有哪几种方案?
两种文具有哪几种方案? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 轴正半轴上一动点,
轴正半轴上一动点,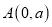 ,
, ,且
,且 、
、 满足
满足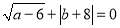 ,
, .
.
(1)求
 的面积;
的面积;(2)若
 ,
, 、
、 为线段
为线段 上的动点,作
上的动点,作 交
交 于
于 ,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB=
,FP平分∠GFC,FN平分∠AFP交x轴于N,记∠FNB= ,求∠BAC(用
,求∠BAC(用 表示);
表示);(3)若
 ,
, 轴于
轴于 ,点
,点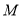 从
从 点出发,在射线
点出发,在射线 上运动,同时另一动点
上运动,同时另一动点 从点
从点 向
向 点运动,到
点运动,到 停止运动,
停止运动,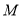 、
、 的速度分别为2个单位/秒、3个单位/秒,当
的速度分别为2个单位/秒、3个单位/秒,当 时,求运动的时间.
时,求运动的时间. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知点A在x正半轴,以点A为圆心作⊙A,点M(4,4)在⊙A上,直线y=﹣
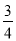 x+b与圆相切于点M,分别交x轴、y轴于B、C两点.
x+b与圆相切于点M,分别交x轴、y轴于B、C两点.(1)直接写出b的值和点B的坐标;
(2)求点A的坐标和圆的半径;
(3)若EF切⊙A于点F分别交AB和BC于G、E,且FE⊥BC,求
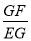 的值.
的值.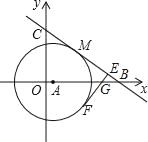
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于点A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连接BE,若AB=2,则BE的最小值为( )

A.
 +1B. 2
+1B. 2 ﹣1C. 3D. 4﹣
﹣1C. 3D. 4﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小长方形卡片(如图①)不重叠的放在一个底面为长方形(长为a厘米,宽为b厘米)的盒子底部(如图②),盒子底面未被卡片覆盖的部分用阴影表示,则图②中两块阴影部分的周长和是( )
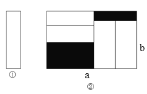
A. 4a厘米B. 4b厘米C. 2(a+b)厘米D. 4(a-b)厘米
相关试题

