【题目】如图,AB为⊙O的直径,点C为半圆上一点,AD平分∠CAB交⊙O于点D 
(1)求证:OD∥AC;
(2)若AC=8,AB=10,求AD.
参考答案:
【答案】
(1)证明:∵AD平分∠CAB交⊙O于点D,
∴∠CAD=∠BAD,
∵OA=OD,
∴∠DAB=∠D,
∴∠CAD=∠D,
∴AC∥OD
(2)解:连接BC,BD,
∵AD平分∠CAB交⊙O于点D,
∴ ![]() =
= ![]() ,
,
∴CE=BE,
∵AB为⊙O的直径,
∴∠C=90°,
∴BC= ![]() =6,
=6,
∴CE=BE=3,
∴OE= ![]() =4,
=4,
∴DE=1,
∴BD= ![]() =
= ![]() ,
,
∴AD= ![]() =3
=3 ![]() .
.
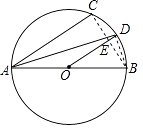
【解析】(1)由AD平分∠CAB交⊙O于点D,得到∠CAD=∠BAD,根据等腰三角形的性质得到∠DAB=∠D,等量代换得到∠CAD=∠D,根据平行线的判定定理即可得到结论;(2)连接BC,BD,根据圆周角定理得到∠C=90°,根据勾股定理即可得到结论.
【考点精析】本题主要考查了圆周角定理的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,除公共边
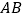 外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使
外,根据下列括号内三角形全等的条件,在横线上添加适当的条件,使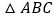 与
与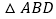 全等:
全等: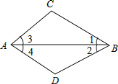
 ________,________
________,________ ;
; ________,________
________,________ ;
;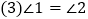 ,________
,________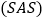 ;
;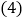 ________,
________,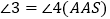 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】点
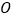 是
是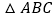 内一点,且点
内一点,且点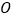 到三边的距离相等,
到三边的距离相等,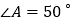 ,则
,则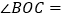 ________.
________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
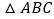 中,若
中,若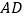 是
是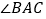 的角平分线,点
的角平分线,点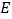 和点
和点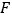 分别在
分别在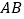 和
和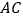 上,且
上,且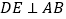 ,垂足为
,垂足为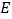 ,
,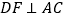 ,垂足为
,垂足为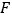 (如图
(如图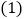 ),则可以得到以下两个结论:
),则可以得到以下两个结论:①
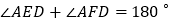 ;②
;②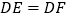 .
.那么在
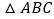 中,仍然有条件“
中,仍然有条件“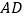 是
是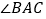 的角平分线,点
的角平分线,点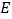 和点
和点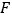 ,分别在
,分别在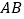 和
和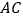 上”,请探究以下两个问题:
上”,请探究以下两个问题: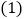 若
若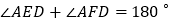 (如图
(如图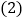 ),则
),则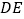 与
与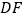 是否仍相等?若仍相等,请证明;否则请举出反例.
是否仍相等?若仍相等,请证明;否则请举出反例.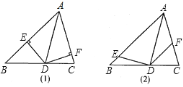
 若
若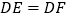 ,则
,则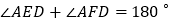 是否成立?(只写出结论,不证明)
是否成立?(只写出结论,不证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元? -
科目: 来源: 题型:
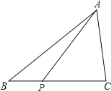
查看答案和解析>>【题目】如图,
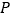 为
为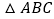 边
边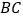 上的一点,且
上的一点,且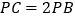 ,已知
,已知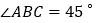 ,
,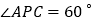 ,则
,则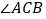 的度数是________
的度数是________ .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形ABCD,点P为BC边上一动点,连接AP,将线段AP绕P点顺时针旋转90°,点A恰好落在直线CD上点E处.
(1)如图1,点E在线段CD上,求证:AD+DE=2AB;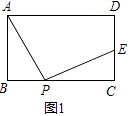
(2)如图2,点E在线段CD的延长线上,且点D为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB.求证:∠APF=∠ADB.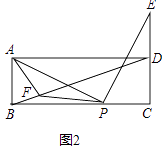
(3)如图3,点E在线段CD上,连接BD,若AB=2,BD∥PE,则DE= . (直接写出结果)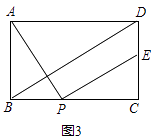
相关试题

