【题目】12月4日为全国法制宣传日,当天某初中组织4名学生参加法制知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录了其中2名参赛学生的得分情况.
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 17 | 3 | 79 |
(1)参赛学生![]() 得72分,他答对了几道题?答错了几道题?
得72分,他答对了几道题?答错了几道题?
(2)参赛学生![]() 说他可以得88分,你认为可能吗?为什么?
说他可以得88分,你认为可能吗?为什么?
参考答案:
【答案】(1)参赛学生![]() 答对了16道题,则答错了4道题;(2)不可能,理由见解析
答对了16道题,则答错了4道题;(2)不可能,理由见解析
【解析】
(1)根据表格中参赛者A的成绩和参赛者B的成绩即可求出每答对一道题得分和每答错一道题扣分,设参赛学生![]() 答对了x道题,则答错了(20-x)道题,根据题意列一元一次方程即可求出结论;
答对了x道题,则答错了(20-x)道题,根据题意列一元一次方程即可求出结论;
(2)设参赛学生![]() 答对了y道题,则答错了(20-y)道题,根据题意列一元一次方程,解出y的值,再根据实际意义判断即可.
答对了y道题,则答错了(20-y)道题,根据题意列一元一次方程,解出y的值,再根据实际意义判断即可.
解:(1)由表格中参赛者A的成绩可知:每答对一道题得100÷20=5分
由表格中参赛者B的成绩可知:每答错一道题扣(17×5-79)÷3=2分
设参赛学生![]() 答对了x道题,则答错了(20-x)道题
答对了x道题,则答错了(20-x)道题
根据题意:5x-2(20-x)=72
解得:x=16
答错了:20-16=4道
答:参赛学生![]() 答对了16道题,则答错了4道题.
答对了16道题,则答错了4道题.
(2)不可能,理由如下
设参赛学生![]() 答对了y道题,则答错了(20-y)道题
答对了y道题,则答错了(20-y)道题
根据题意:5y-2(20-y)=88
解得:y=![]()
由题意可知:y是整数
∴参赛学生![]() 不可能得88分.
不可能得88分.
-
科目: 来源: 题型:
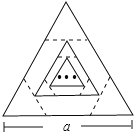
查看答案和解析>>【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A.
 B.
B. 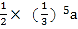 C.
C. 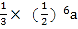 D.
D. 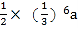
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
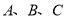 都在直线
都在直线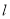 上,
上,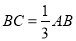 ,
,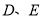 分别为
分别为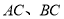 中点,直线
中点,直线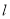 上所有线段的长度之和为19,则
上所有线段的长度之和为19,则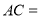 __________.
__________. -
科目: 来源: 题型:
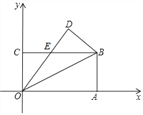
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(I)证明:EO=EB;
(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
设某一商品的标价为
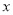 元:
元:(1)当
 元,按方式二应付多少钱.
元,按方式二应付多少钱.(2)当
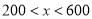 时,
时,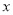 取何值两种方式的优惠相同.
取何值两种方式的优惠相同. -
科目: 来源: 题型:
查看答案和解析>>【题目】点
 在数轴上所对应的数分别是
在数轴上所对应的数分别是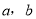 ,其中
,其中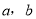 满足
满足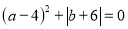 .
.(1)求
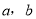 的值;
的值;(2)数轴上有一点
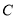 ,使得
,使得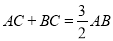 ,求点
,求点 所对应的数;
所对应的数;(3)点
 为
为 中点,
中点, 为原点,数轴上有一动点
为原点,数轴上有一动点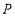 ,求
,求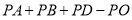 的最小值及点
的最小值及点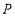 所对应的数的取值范围.
所对应的数的取值范围.
相关试题

