【题目】已知点![]() 都在直线
都在直线![]() 上,
上,![]() ,
,![]() 分别为
分别为![]() 中点,直线
中点,直线![]() 上所有线段的长度之和为19,则
上所有线段的长度之和为19,则![]() __________.
__________.
参考答案:
【答案】![]() 或4
或4
【解析】
根据点C与点B的位置关系分类讨论,分别画出对应的图形,推出各线段与AC的关系,根据直线![]() 上所有线段的长度之和为19,列出关于AC的方程即可求出AC.
上所有线段的长度之和为19,列出关于AC的方程即可求出AC.
解:若点C在点B左侧时,如下图所示:
![]()
∵![]()
∴![]()
∴BC=![]() ,AB=
,AB=![]()
∵点![]() 分别为
分别为![]() 中点
中点
∴AD=DC=![]() ,CE=BE=
,CE=BE=![]()
∴AE=AC+CE=![]() ,DE=DC+CE=
,DE=DC+CE=![]() ,DB=DC+CB=AC
,DB=DC+CB=AC
∵直线![]() 上所有线段的长度之和为19
上所有线段的长度之和为19
∴AD+AC+AE+AB+DC+DE+DB+CE+CB+EB=19
即![]() +AC+
+AC+![]() +
+![]() +
+![]() +
+![]() +AC+
+AC+![]() +
+![]() +
+![]() =19
=19
解得:AC=![]() ;
;
若点C在点B右侧时,如下图所示:
∵![]()
∴![]()
∴BC=![]() ,AB=
,AB=![]()
∵点![]() 分别为
分别为![]() 中点
中点
∴AD=DC=![]() ,CE=BE=
,CE=BE=![]()
∴AE=AC-CE=![]() ,DE=DC-CE=
,DE=DC-CE=![]() ,DB=DC-CB=
,DB=DC-CB=![]()
∵直线![]() 上所有线段的长度之和为19
上所有线段的长度之和为19
∴AD+AC+AE+AB+DC+DE+DB+CE+CB+EB=19
即![]() +AC+
+AC+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() +
+![]() =19
=19
解得:AC=![]()
综上所述:AC=![]() 或4.
或4.
故答案为:![]() 或4.
或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需绕行B地,已知B地位于A地北偏东67°方向,距离A地520km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)
(参考数据:sin67°≈
 ,cos67°≈
,cos67°≈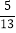 ,tan67°≈
,tan67°≈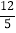 ,
,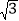 ≈1.73)
≈1.73)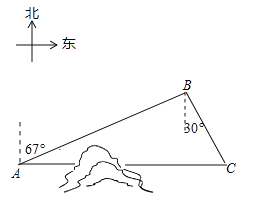
-
科目: 来源: 题型:
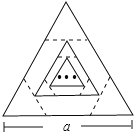
查看答案和解析>>【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A.
 B.
B. 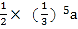 C.
C. 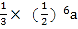 D.
D. 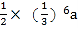
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A
B
载客量(人/辆)
45
30
租金(元/辆)
400
280
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆)
载客量(人)
租金(元)
A
x
45x
400x
B
5-x
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】12月4日为全国法制宣传日,当天某初中组织4名学生参加法制知识竞赛,共设20道选择题,各题分值相同,每题必答,下表记录了其中2名参赛学生的得分情况.
参赛者
答对题数
答错题数
得分
A
20
0
100
B
17
3
79
(1)参赛学生
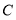 得72分,他答对了几道题?答错了几道题?
得72分,他答对了几道题?答错了几道题?(2)参赛学生
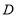 说他可以得88分,你认为可能吗?为什么?
说他可以得88分,你认为可能吗?为什么? -
科目: 来源: 题型:
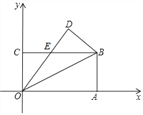
查看答案和解析>>【题目】如图,在平面直角坐标系中,长方形OABC的顶点A、C分别在x轴、y轴的正半轴上.点B的坐标为(8,4),将该长方形沿OB翻折,点A的对应点为点D,OD与BC交于点E.
(I)证明:EO=EB;
(Ⅱ)点P是直线OB上的任意一点,且△OPC是等腰三角形,求满足条件的点P的坐标;
(Ⅲ)点M是OB上任意一点,点N是OA上任意一点,若存在这样的点M、N,使得AM+MN最小,请直接写出这个最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】元旦期间某商店进行促销活动,活动方式有如下两种:
方式一:每满200元减50元;
方式二:若标价不超过400元时,打8折;若标价超过400元,则不超过400元的部分打8折,超出400元的部分打6折.
设某一商品的标价为
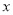 元:
元:(1)当
 元,按方式二应付多少钱.
元,按方式二应付多少钱.(2)当
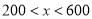 时,
时,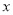 取何值两种方式的优惠相同.
取何值两种方式的优惠相同.
相关试题

