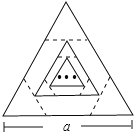
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
连接AD、DB、DF,求出∠AFD=∠ABD=90°,根据HL证两三角形全等得出∠FAD=60°,求出AD∥EF∥GI,过F作FZ⊥GI,过E作EN⊥GI于N,得出平行四边形FZNE得出EF=ZN=![]() a,求出GI的长,求出第一个正六边形的边长是
a,求出GI的长,求出第一个正六边形的边长是![]() a,是等边三角形QKM的边长的
a,是等边三角形QKM的边长的![]() ;同理第二个正六边形的边长是等边三角形GHI的边长的
;同理第二个正六边形的边长是等边三角形GHI的边长的![]() ;求出第五个等边三角形的边长,乘以
;求出第五个等边三角形的边长,乘以![]() 即可得出第六个正六边形的边长.
即可得出第六个正六边形的边长.
连接AD、DF、DB.
∵六边形ABCDEF是正六边形,
∴∠ABC=∠BAF=∠AFE,AB=AF,∠E=∠C=120°,EF=DE=BC=CD,
∴∠EFD=∠EDF=∠CBD=∠BDC=30°,
∵∠AFE=∠ABC=120°,
∴∠AFD=∠ABD=90°,
在Rt△ABD和RtAFD中
![]()
∴Rt△ABD≌Rt△AFD(HL),
∴∠BAD=∠FAD=![]() ×120°=60°,
×120°=60°,
∴∠FAD+∠AFE=60°+120°=180°,
∴AD∥EF,
∵G、I分别为AF、DE中点,
∴GI∥EF∥AD,
∴∠FGI=∠FAD=60°,
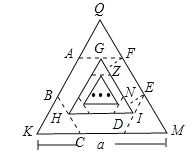
∵六边形ABCDEF是正六边形,△QKM是等边三角形,
∴∠EDM=60°=∠M,
∴ED=EM,
同理AF=QF,
即AF=QF=EF=EM,
∵等边三角形QKM的边长是a,
∴第一个正六边形ABCDEF的边长是![]() a,即等边三角形QKM的边长的
a,即等边三角形QKM的边长的![]() ,
,
过F作FZ⊥GI于Z,过E作EN⊥GI于N,
则FZ∥EN,
∵EF∥GI,
∴四边形FZNE是平行四边形,
∴EF=ZN=![]() a,
a,
∵GF=![]() AF=
AF=![]() ×
×![]() a=
a=![]() a,∠FGI=60°(已证),
a,∠FGI=60°(已证),
∴∠GFZ=30°,
∴GZ=![]() GF=
GF=![]() a,
a,
同理IN=![]() a,
a,
∴GI=![]() a+
a+![]() a+
a+![]() a=
a=![]() a,即第二个等边三角形的边长是
a,即第二个等边三角形的边长是![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第二个正六边形的边长是![]() ×
×![]() a;
a;
同理第第三个等边三角形的边长是![]() ×
×![]() a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是
a,与上面求出的第一个正六边形的边长的方法类似,可求出第三个正六边形的边长是![]() ×
×![]() ×
×![]() a;
a;
同理第四个等边三角形的边长是![]() ×
×![]() ×
×![]() a,第四个正六边形的边长是
a,第四个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第五个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() a,第五个正六边形的边长是
a,第五个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a;
a;
第六个等边三角形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,第六个正六边形的边长是
a,第六个正六边形的边长是![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() ×
×![]() a,
a,
即第六个正六边形的边长是![]() ×
×![]() a,
a,
故选A.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题的逆命题成立的是( ).
A.全等三角形的对应角相等
B.若三角形的三边满足
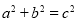 ,则该三角形是直角三角形
,则该三角形是直角三角形C.对顶角相等
D.同位角互补,两直线平行
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,抛物线
 ( a≠0)经过原点,顶点为A(h,k)(h≠0).
( a≠0)经过原点,顶点为A(h,k)(h≠0).(1)当h=1,k=2时,求抛物线的解析式;
(2)若抛物线
 (t≠0)也经过A点,求a与t之间的关系式;
(t≠0)也经过A点,求a与t之间的关系式;(3)当点A在抛物线
 上,且-2≤h<1时,求a的取值范围.
上,且-2≤h<1时,求a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列判断错误的是( )

A. 如果∠2=∠4,那么AB∥CD B. 如果∠1=∠3,那么AB∥CD
C. 如果∠BAD+∠D=180°,那么AB∥CD D. 如果∠BAD+∠B=180,那么AD∥CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式和不等式组,并把它的解集在数轴上表示出来.
(1)

(2)

(3)

-
科目: 来源: 题型:
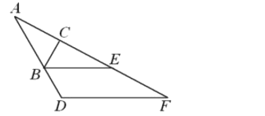
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=36°,△ABC的外角∠CBD的平分线BE交AC的延长线于点E.
(1)求∠CBE的度数;
(2)点F是AE延长线上一点,过点F作∠AFD=27°,交AB的延长线于点D.求证:BE∥DF.
-
科目: 来源: 题型:
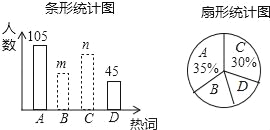
查看答案和解析>>【题目】2016年3月全国两会胜利召开,某数学兴趣小组就两会期间出现频率最高的热词:A脱贫攻坚.B.绿色发展.C.自主创新.D.简政放权等热词进行了抽样调查,每个同学只能从中选择一个“我最关注”的热词,如图是根据调查结果绘制的两幅不完整的统计图.
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了 名同学;
(2)条形统计图中,m= ,n= ;
(3)扇形统计图中,热词B所在扇形的圆心角的度数是 ;
(4)从该校学生中随机抽取一个最关注热词D的学生的概率是多少?
相关试题

