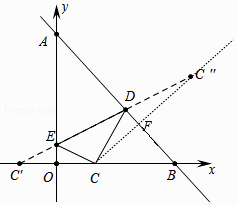
【题目】如图，已知点C（1，0），直线y=﹣x+7与两坐标轴分别交于A、B两点，D、E分别是AB，OA上的动点，当△CDE周长最小时，点D坐标为 ．

参考答案：

【答案】（ ， ）
【解析】解：如图，点C关于OA的对称点C′（﹣1，0），点C关于直线AB的对称点C″，
∵直线AB的解析式为y=﹣x+7，
∴直线CC″的解析式为y=x﹣1，
由 解得 ，
∴F（4，3），
∵F是CC″中点，
∴可得C″（7，6）．
连接C′C″与AO交于点E，与AB交于点D，此时△DEC周长最小，
∵C′（﹣1，0），C″（7，6），
∴设直线DE的解析式为y=kx+b，
∴ ，
解得 ，
∴直线DE的解析式为y= x+ ，
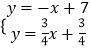由 解得 ，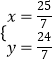
∴点D坐标为（ ， ），
所以答案是（ ， ）．

【考点精析】解答此题的关键在于理解一次函数的性质的相关知识，掌握一般地，一次函数y=kx+b有下列性质：（1）当k>0时，y随x的增大而增大（2）当k<0时，y随x的增大而减小，以及对一次函数的图象和性质的理解，了解一次函数是直线，图像经过仨象限；正比例函数更简单,经过原点一直线；两个系数k与b,作用之大莫小看，k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减；k为负来左下展,变化规律正相反；k的绝对值越大,线离横轴就越远．

关闭