【题目】如图，在平面直角坐标系中，菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，顶点C的坐标为（﹣ ，3），反比例函数y= 的图象与菱形对角线AO交于D点，连接BD，当BD⊥x轴时，k的值是（ ）
A.4
B.﹣4
C.2
D.﹣2

参考答案：

【答案】B
【解析】解：延长AC交y轴于E，如图，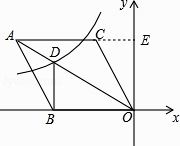
∵菱形ABOC的顶点O在坐标原点，边BO在x轴的负半轴上，
∴AC∥OB，
∴AE⊥y轴，
∵C（﹣ ，3），
∴OC= =2 ，∠EOC=30°，
∴∠BOC=60°，
∵四边形OBAC为菱形，
∴∠AOB=∠AOC，OB=OC=2 ，AC∥OB，
∴∠COE=30°，
在Rt△BDO中，
∵BD= OB=2，
∴D点坐标为（﹣2 ，2），
∵反比例函数y= 的图象经过点D，
∴k=﹣2 ×2=﹣4 ，
故选B．
延长AC交y轴于E，由已知得到∠COE=30°，OC=2 如图，根据菱形的性质得AC∥OB，则AE⊥y轴，接着根据菱形的性质得OB=OC=2 ，∠BOA=30°，于是在Rt△BDO中可计算出BD=2，所以D点坐标为（﹣2 ，2），然后利用反比例函数图象上点的坐标特征可求出k的值．

关闭