【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点![]() 在
在![]() 的边
的边![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 且
且![]() ,在
,在![]() 上截取
上截取![]() ,再作
,再作![]() 交线段
交线段![]() 于点
于点![]() .
.

实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现![]() ,
,![]() ,请说明理由;
,请说明理由;
探究应用
(3)缜密小组在勤奋小组探究的基础上,测得![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)线段![]() 的长为9
的长为9
【解析】
(1)以![]() 为圆心,任意为半径画弧,交
为圆心,任意为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,同等长为半径画弧,交
为圆心,同等长为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径,与前弧交于
为半径,与前弧交于![]() ,连接
,连接![]() 并延长至
并延长至![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径,与
长为半径,与![]() 交于
交于![]() ,以
,以![]() 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交![]() 于点
于点![]() ,以
,以![]() 为圆心,同等长为半径,交
为圆心,同等长为半径,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径交前弧于
长为半径交前弧于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ;
;
(2)根据平行和(1)中作的图证明![]() ,根据全等得出对应边相等、再根据对应角相等得出平行;
,根据全等得出对应边相等、再根据对应角相等得出平行;
(3)由(2)的全等得出![]() ,再根据线段之间的关系算出
,再根据线段之间的关系算出![]() .
.
(1)以![]() 为圆心,任意为半径画弧,交
为圆心,任意为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,同等长为半径画弧,交
为圆心,同等长为半径画弧,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径,与前弧交于
为半径,与前弧交于![]() ,连接
,连接![]() 并延长至
并延长至![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径,与
长为半径,与![]() 交于
交于![]() ,以
,以![]() 为圆心,任意长为半径画弧交
为圆心,任意长为半径画弧交![]() 于点
于点![]() ,以
,以![]() 为圆心,同等长为半径,交
为圆心,同等长为半径,交![]() 于
于![]() ,以
,以![]() 为圆心,
为圆心,![]() 长为半径交前弧于
长为半径交前弧于![]() ,连接
,连接![]() 并延长交
并延长交![]() 于
于![]() ,如图为所求图形:
,如图为所求图形:

(2)理由如下:
在![]() 和
和![]() 中,
中,

∴![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.
(3)由(2)得,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴线段![]() 的长为9.
的长为9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,
中, ,
, ,
, .点
.点 从点
从点 出发,以
出发,以 的速度沿
的速度沿 向点
向点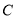 运动,设点
运动,设点 的运动时间为
的运动时间为 .
.(1)
 ________
________ ;(用含
;(用含 的代数式表示)
的代数式表示)(2)如图1,当
 为何值时,
为何值时, ?并说明理由;
?并说明理由;
(3)如图2,当点
 从点
从点 开始运动,同时,点
开始运动,同时,点 从点
从点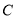 出发,以
出发,以 的速度沿
的速度沿 向点
向点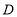 运动,当
运动,当 运动到点
运动到点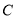 或点
或点 运动到点
运动到点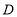 时运动停止.是否存在这样的
时运动停止.是否存在这样的 值,使得
值,使得 与
与 全等?若存在,请求出
全等?若存在,请求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,点P是直线l3上一动点
(1)如图1,当点P在线段CD上运动时,∠PAC,∠APB,∠PBD之间存在什么数量关系?请你猜想结论并说明理由.
(2)当点P在C、D两点的外侧运动时(P点
 与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
与点C、D不重合,如图2和图3),上述(1)中的结论是否还成立?若不成立,请直接写出∠PAC,∠APB,∠PBD之间的数量关系,不必写理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司招聘职员两名,对甲、乙、丙、丁四名候选人进行了笔试和面试,各项成绩满分均为100分,然后再按笔试占60%、面试占40%计算候选人的综合成绩(满分为100分).
他们的各项成绩如下表所示:
候选人
笔试成绩/分
面试成绩/分
甲
90
88
乙
84
92
丙
x
90
丁
88
86
(1)直接写出这四名候选人面试成绩的中位数;
(2)现得知候选人丙的综合成绩为87.6分,求表中x的值;
(3)求出其余三名候选人的综合成绩,并以综合成绩排序确定所要招聘的前两名的人选.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)2﹣(+4 )+(﹣1
)+(﹣1  )
)
(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些相关的代数等式,这些等式可用于代数式的证明或求一些不规则图形的面积.
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为
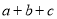 的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;
的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;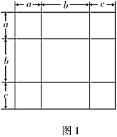
(2)已知三个数
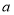 ,
,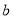 ,
,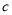 满足
满足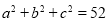 ,
,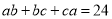 ,利用(1)中发现的结论可直接写出
,利用(1)中发现的结论可直接写出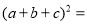 ________;
________;(3)如图2,是将两个边长分别为
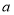 和
和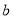 的正方形拼在一起,
的正方形拼在一起,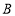 ,
,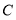 ,
,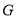 三点在同一直线上,连接
三点在同一直线上,连接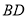 和
和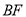 ,若两正方形的边长满足
,若两正方形的边长满足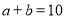 ,
,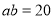 ,请求出阴影部分的面积.
,请求出阴影部分的面积.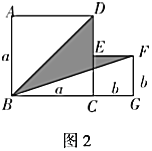
相关试题

