【题目】把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些相关的代数等式,这些等式可用于代数式的证明或求一些不规则图形的面积.
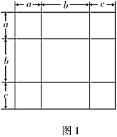
(1)如图1,是将几个面积不等的小正方形与小长方形拼成一个边长为![]() 的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;
的正方形,若把这个大正方形的面积直接用边长表示,其面积是________;若把这个大正方形的面积用分割成的小正方形或小矩形的面积表示时,其面积是________;无论怎样表示,面积不变,所以,可得等式是________;并用多项式的乘法公式说明该等式成立;
(2)已知三个数![]() ,
,![]() ,
,![]() 满足
满足![]() ,
,![]() ,利用(1)中发现的结论可直接写出
,利用(1)中发现的结论可直接写出![]() ________;
________;
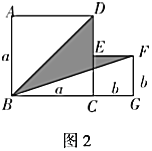
(3)如图2,是将两个边长分别为![]() 和
和![]() 的正方形拼在一起,
的正方形拼在一起,![]() ,
,![]() ,
,![]() 三点在同一直线上,连接
三点在同一直线上,连接![]() 和
和![]() ,若两正方形的边长满足
,若两正方形的边长满足![]() ,
,![]() ,请求出阴影部分的面积.
,请求出阴影部分的面积.
参考答案:
【答案】(1)![]() ,
,![]() ,
, ![]() ,理由见解析;(2)100;(3)20
,理由见解析;(2)100;(3)20
【解析】
(1)①根据正方形的面积等于边长的平方,寻找出大正方形的边长即可;②将大正方形进行割补法算出每一部分分割的图形面积再相加即可;③根据面积不变性即可得到等量关系,根据整体思想利用完全平方公式即可证明.
(2)根据(1)中![]() ,代入计算即可;
,代入计算即可;
(3)根据割补法表示出两个正方形的面积减去两个空白三角形的面积即是阴影部分的面积,再代入计算.
解:(1)①根据图形知:大正方形的边长为![]() ,所以面积是
,所以面积是![]() ;
;
②将大正方形拆分成小的正方形和长方形的面积和:
![]()

③根据面积不变性得出:![]()
理由如下:
左边![]()
![]()
![]()
![]() 右边.
右边.
∴![]() 成立.
成立.
(2)根据(1)结论:![]()
∵![]() ,
,![]()
∴![]()
故答案为:100
(3)阴影部分的面积![]()
![]()
![]()
![]() .
.
故阴影部分的面积为:20
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:在综合实践课上,老师让同学们在已知三角形的基础上,经过画图,探究三角形边之间存在的关系.如图,已知点
 在
在 的边
的边 的延长线上,过点
的延长线上,过点 作
作 且
且 ,在
,在 上截取
上截取 ,再作
,再作 交线段
交线段 于点
于点 .
.
实践操作
(1)尺规作图:作出符合上述条件的图形;
探究发现
(2)勤奋小组在作出图形后,发现
 ,
, ,请说明理由;
,请说明理由;探究应用
(3)缜密小组在勤奋小组探究的基础上,测得
 ,
, ,求线段
,求线段 的长.
的长. -
科目: 来源: 题型:
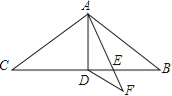
查看答案和解析>>【题目】如图,在△ABC中,AB=AC=11,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,则DF的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣3)2﹣(+4 )+(﹣1
)+(﹣1  )
)
(2)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中, ,
, 是
是 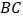 的中点.将
的中点.将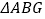 沿
沿 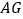 对折至
对折至 , 延长
, 延长 交
交  于点
于点 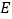 ,则
,则 的长是____.
的长是____.
-
科目: 来源: 题型:
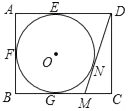
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=4,AD=5,AD,AB,BC分别与⊙O相切于E,F,G三点,过点D作⊙O的切线BC于点M,切点为N,则DM的长为( )
A.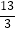
B.
C.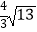
D.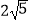
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表是橘子的销售额随橘子卖出质量的变化表:
质量/千克
1
2
3
4
5
6
7
8
9
…
销售额/元
2
4
6
8
10
12
14
16
18
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当橘子卖出5千克时,销售额是_______元.
(3)如果用
 表示橘子卖出的质量,
表示橘子卖出的质量, 表示销售额,按表中给出的关系,
表示销售额,按表中给出的关系, 与
与 之间的关系式为______.
之间的关系式为______.(4)当橘子的销售额是100元时,共卖出多少千克橘子?
相关试题

