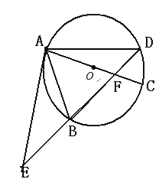
【题目】(本题满分8分)如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,
∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)在(2)的条件下,已知AF=4,CF=2,求AE的长.
参考答案:
【答案】(1)见解析;(2)见解析;(3)AE=4![]()
【解析】试题分析:(1)连接CD,根据直径所对的圆周角为直角得出∠ADB+∠EDC=90°,根据同弧所对的圆周角相等得出∠BAC=∠EDC,然后结合已知条件得出∠EAB+∠BAC=90°,从而说明切线;(2)连接BC,根据直径的性质得出∠ABC=90°,根据B是EF的中点得出AB=EF,即∠BAC=∠AFE,则得出三角形相似;(3)根据三角形相似得出![]() ,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入
,根据AF和CF的长度得出AC的长度,然后根据EF=2AB代入![]() 求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
求出AB和EF的长度,最后根据Rt△AEF的勾股定理求出AE的长度.
试题解析:(1)证明:如答图1,连接CD, ∵AC是⊙O的直径,∴∠ADC=90°.
∴∠ADB+∠EDC=90°.
∵∠BAC=∠EDC,∠EAB=∠ADB, ∴∠BAC=∠EAB+∠BAC=90°.∴EA是⊙O的切线.

(2)证明:如答图2,连接BC, ∵AC是⊙O的直径,∴∠ABC=90°.∴∠CBA=∠ABC=90°.
∵B是EF的中点,∴在Rt△EAF中,AB=BF. ∴∠BAC=∠AFE. ∴△EAF∽△CBA.

(3)∵△EAF∽△CBA,∴![]() . ∵AF=4,CF=2, ∴AC=6,EF=2AB.
. ∵AF=4,CF=2, ∴AC=6,EF=2AB.
∴![]() ,解得AB=2
,解得AB=2![]() .∴EF=4
.∴EF=4![]() .
.
∴AE=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在坐标平面内有下列三条直线:
①经过点(0,2)且平行于x轴的直线;
②直线y=2x﹣8;
③经过点(0,12)且平行于直线y=﹣2x的直线,
其中经过点(5,2)但不经过第三象限的直线共有( )
A.0条
B.1条
C.2条
D.3条 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行于x轴的直线l与y轴、直线y=3x、直线y=x分别交于点A,B,C.则下列结论正确的个数有( )
①∠AOB+∠BOC=45°;②BC=2AB;③OB2=10AB2;④OC2=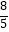 OB2 .
OB2 . 
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:a2a4= .
-
科目: 来源: 题型:
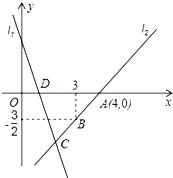
查看答案和解析>>【题目】如图,直线l1的表达式为y=﹣3x+3,且直线l1与x轴交与点D,直线l2经过点A,B,且与直线l1交于点C,则△BDC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的四条线段是成比例线段的是( )
A. 4cm、4cm、5cm、6cmB. 1cm、2cm、3cm、5cm
C. 3cm、4cm、5cm、6cmD. 1cm、2cm、2cm、4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧
 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是 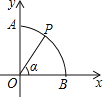
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
相关试题

