【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
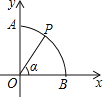
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
参考答案:
【答案】C
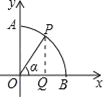
【解析】过P作PQ⊥OB,交OB于点Q,在直角三角形OPQ中,利用锐角三角函数定义表示出OQ与PQ,即可确定出P的坐标.
解:过P作PQ⊥OB,交OB于点Q,
在Rt△OPQ中,OP=1,∠POQ=α,
∴sinα=![]() ,cosα=
,cosα=![]() ,即PQ=sinα,OQ=cosα,
,即PQ=sinα,OQ=cosα,
则P的坐标为(cosα,sinα),
故选C.
“点睛”此题考查了解直角三角形,以及坐标与图形性质,熟练掌握锐角三角函数定义是解本题的关键.
-
科目: 来源: 题型:
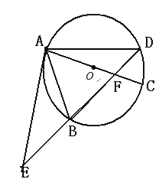
查看答案和解析>>【题目】(本题满分8分)如图,⊙O的直径AC与弦BD相交于点F,点E是DB延长线上一点,
∠EAB=∠ADB.
(1)求证:EA是⊙O的切线;
(2)已知点B是EF的中点,求证:以A、B、C为顶点的三角形与△AEF相似;
(3)在(2)的条件下,已知AF=4,CF=2,求AE的长.
-
科目: 来源: 题型:
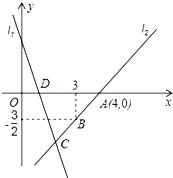
查看答案和解析>>【题目】如图,直线l1的表达式为y=﹣3x+3,且直线l1与x轴交与点D,直线l2经过点A,B,且与直线l1交于点C,则△BDC的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组中的四条线段是成比例线段的是( )
A. 4cm、4cm、5cm、6cmB. 1cm、2cm、3cm、5cm
C. 3cm、4cm、5cm、6cmD. 1cm、2cm、2cm、4cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( )
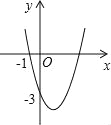
A. ﹣3<P<﹣1 B. ﹣6<P<0 C. ﹣3<P<0 D. ﹣6<P<﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:2x2﹣2=( )
A.2(x2﹣1)
B.2(x2+1)
C.2(x﹣1)2
D.2(x+1)(x﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为__cm2.

相关试题

