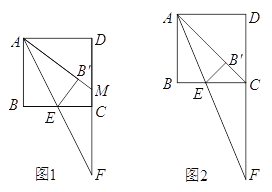
【题目】如图,正方形ABCD的边长为12,点E是射线BC上的一个动点,连接AE并延长,交射线DC于点F,将△ABE沿直线AE翻折,点B落在点B'处.
(1)当![]() =1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
=1时,如图1,延长A B',交CD于点M,①CF的长为 ;②求证:AM=FM.
(2)当点B'恰好落在对角线AC上时,如图2,此时CF的长为 ; ![]() = .
= .
(3)当![]() =3时,求∠DA B'的正弦值.
=3时,求∠DA B'的正弦值.
参考答案:
【答案】(1)①CF的长为12;②证明见解析;
2)CF的长为12![]() ,
, ![]() =
=![]() ;
;
(3)当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.
【解析】解:(1)①CF的长为 12 ;
②证明:∵四边形ABCD为正方形,
∴AB∥CD,∴∠ F=∠ BAF,
由折叠可知:∠ BAF=∠ MAF,
∴∠ F=∠ MAF,∴AM=FM.
(2)CF的长为12![]() ;
;
![]() =
=![]() .
.
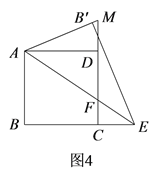
(3)①当点E在线段BC上时,如图3,
 A B'的延长线交CD于点M,易证:△ABE∽△FCE,
A B'的延长线交CD于点M,易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
由(1)②证明可知:
AM=FM.设DM=x,则MC=12-x,则AM=FM=16-x,
在Rt△ADM中, ![]() ,
,
 即(16-x)2=122+x2,解得:x=
即(16-x)2=122+x2,解得:x=![]() ,
,
则16-x=16-![]() =
=![]() ,
,
∴sin∠DA B'=![]() =
=![]() .
.
②当点E在BC的延长线上时,如图4,
易证:△ABE∽△FCE,
∴![]() ,即
,即![]() ,∴CF=4,
,∴CF=4,
则DF=12-4=8,设DM=x,则AM=FM=8+x,
在Rt△ADM中, ![]() ,
,
即(8+x)2=122+x2,解得:x=5,则AM=8+x=13,
∴sin∠DA B'=![]() =
=![]() .
.
综上所述:当![]() 时,∠DA B'的正弦值为
时,∠DA B'的正弦值为![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(m,1)与点B(3,n)关于原点对称,则m+n=_________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若∠A=95°,∠B=40°,则∠C的度数为( )
A.35°
B.40°
C.45°
D.50° -
科目: 来源: 题型:
查看答案和解析>>【题目】一家商场将某种型号的彩电按物价部门核准的最高售价提高30%,然后标出”“大酬宾,八折优惠,经顾客投诉后,执法部门按所得的非法收入的10倍处以每台1000元的罚款,则每台的彩电按物价部门核准的最高售价是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+3经过点A,B,C,已知A(-1,0),B(3,0).
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一点,过点P作y轴的平行线,交抛物线于点D,当△BDC的面积最大时,求点P的坐标;
(3)如图2,在(2)的条件下,延长DP交x轴于点F,M(m,0)是x轴上一动点,N 是线段DF上一点,当△BDC的面积最大时,若∠MNC=90°,请直接写出实数m的取值范围.

-
科目: 来源: 题型:
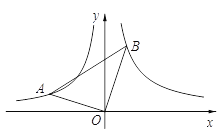
查看答案和解析>>【题目】如图,∠ AOB=90°,且点A,B分别在反比例函数
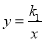 (x<0),
(x<0),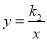 (x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.(1)求k1,k2的值;
(2)连接AB,求tan∠ OBA的值.
-
科目: 来源: 题型:
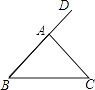
查看答案和解析>>【题目】如图,△ABC中,AB=AC,与∠BAC相邻的外角为80°,则∠B=度.
相关试题

