【题目】已知:如图,M、N分别为两平行线AB、CD上两点,点E位于两平行线之间,试探究:∠MEN与∠AME和∠CNE之间有何关系?并说明理由.

参考答案:
【答案】(1)当点E在MN上时,∠MEN=∠CNE+∠AME=180°. 证明见解析;(2)当点E在MN左侧时,∠MEN=∠AME+∠CNE.证明见解析;(3)当点E在MN右侧时,∠MEN=360°-(∠AME+∠CNE).证明见解析;
【解析】
连结MN,根据平行线的性质,分三种情况讨论:
(1)当点E在MN上时,∠MEN=∠CNE+∠AME=180°.
(2)当点E在MN左侧时,∠MEN=∠AME+∠CNE.
(3)当点E在MN右侧时,∠MEN=360°-(∠AME+∠CNE).
连结MN,分三种情况:
点E在MN上;⑵点E在MN左侧;⑶点E在MN右侧.如图所示:

(1)当点E在MN上时,∠MEN=∠CNE+∠AME=180°.
证明:∵AB∥CD,
∴∠CNE+∠AME=180°.
又∵∠MEN是平角,
∴∠∠MEN=180°,
∴∠MEN=∠AME+∠CNE=180°.
(2)当点E在MN左侧时,∠MEN=∠AME+∠CNE.
证明:过点E作![]() ∥
∥![]()
∴![]() ,
,![]()
∵![]()
∴∠MEN=∠AME+∠CNE.
(3)当点E在MN右侧时,∠MEN=360°-(∠AME+∠CNE).
证明:过点E作EG∥AB
∴![]() ,
,![]()
∵![]()
∴∠MEN=360°-(∠AME+∠CNE)
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两同学的家与某科技馆的距离均为4000m.甲、乙两人同时从家出发去科技馆,甲同学先步行800m,然后乘公交车,乙同学骑自行车.已知乙骑自行车的速度是甲步行速度的4倍,公交车的速度是乙骑自行车速度的2倍,结果甲同学比乙同学晚到2.5min.求乙到达科技馆时,甲离科技馆还有多远.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于函数
 的四个命题:①当
的四个命题:①当 时,
时,  有最小值10;②
有最小值10;② 为任意实数,
为任意实数,  时的函数值大于
时的函数值大于 时的函数值;③若
时的函数值;③若 ,且
,且 是整数,当
是整数,当 时,
时,  的整数值有
的整数值有 个;④若函数图象过点
个;④若函数图象过点 和
和 ,其中
,其中 ,
,  ,则
,则 .其中真命题的序号是( )
.其中真命题的序号是( )A. ① B. ② C. ③ D. ④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
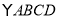 中,对角线
中,对角线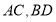 交于点
交于点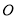 ,
,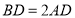 ,
,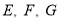 分别是
分别是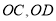 ,
,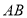 的中点.下列结论正确的是( )
的中点.下列结论正确的是( )①
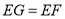 ;②
;②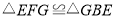 ;③
;③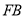 平分
平分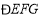 ;④
;④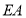 平分
平分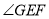 ;⑤四边形
;⑤四边形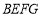 是菱形.
是菱形.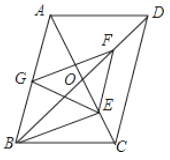
A.③⑤B.①②④C.①②③④D.①②③④⑤
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某长方形广场的四个角都有一个半径相同的四分之一圆形的草地,若圆形的半径为x米,长方形长为a米,宽为b米
(1)分别用代数式表示草地和空地的面积;
(2)若长方形长为300米,宽为200米,圆形的半径为10米,求广场空地的面积(计算结果保留到整数)

-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含30°和45°角的三角板ABC和DEF叠合在一起,边BC与EF重合,BC=EF=12cm(如图1),点G为边BC(EF)的中点,边FD与AB相交于点H,此时线段BH的长是____.现将三角板DEF绕点G按顺时针方向旋转(如图2),在∠CGF从0°到60°的变化过程中,点H相应移动的路径长共为_________.(结果保留根号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=
 .
.(1)写出此二次函数图象的对称轴;
(2)在如图中建立平面直角坐标系,并画出该函数的图象.(列表、描点、连线)
(3)结合图象回答问题:
①当x的取值范围是 时,y≤0?
②将此抛物线向 平移 个单位时,它与x轴有且只有一个公共点.

相关试题

