【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为![]() 和
和![]() ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
参考答案:
【答案】(1)甲种树苗买200株,则乙种树苗买100株;(2)应买225株甲种树苗,75株乙种树苗时该小区的空气净华指数之和不低于90,费用最小为20250元.
【解析】
(1)设甲种树苗买x株,则乙种树苗买(300-x)株,根据“甲树苗的费用+乙树苗的费用=21000”作为相等关系列方程即可求解;
(2)设买x株甲种树苗,(300-x)株乙种树苗时该小区的空气净化指数之和不低于90,先根据“空气净化指数之和不低于90”列不等式求得x的取值范围,再根据题意用x表示出费用,列成一次函数的形式,利用一次函数的单调性来讨论费用的最小值,即函数最小值问题.
(1)设甲种树苗买x株,则乙种树苗买(300-x)株
60x+90(300-x)=21000
x=200
300-200=100
答:甲种树苗买200株,则乙种树苗买100株.
(2)设买x株甲种树苗,(300-x)株乙种树苗时该小区的空气净华指数之和不低于90
0.2x+0.6(300-x)≥90
0.2x+180-0.6x≥90
-0.4x≥-90
x≤225
此时费用y=60x+90(300-x)
y=-30x+27000
∵y是x的一次函数,y随x的增大而减少
∴当x最大=225时,y最小=-30×225+27000=20250(元)
即应买225株甲种树苗,75株乙种树苗时该小区的空气净华指数之和不低于90,费用最小为20250元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
 .
. (1)
 满足何条件时,y随x的增大而减小;
满足何条件时,y随x的增大而减小;(2)
 满足何条件时,图像经过第一、二、四象限;
满足何条件时,图像经过第一、二、四象限;(3)
 满足何条件时,它的图像与y轴的交点在x轴的上方.
满足何条件时,它的图像与y轴的交点在x轴的上方. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1:y=
 x-3与x轴,y轴分别交于点A和点B.
x-3与x轴,y轴分别交于点A和点B.(1)求点A和点B的坐标;
(2)将直线l1向上平移6个单位后得到直线l2,求直线l2的函数解析式;
(3)设直线l2与x轴的交点为M,则△MAB的面积是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据爱因斯坦的相对论,当地面上经过1秒钟时,宇宙飞船内只经过
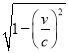 秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论.
秒.公式内的v是指宇宙飞船的速度,c是指光速(约 30万千米/秒),假定有一对亲兄弟,哥哥23岁,弟弟 20岁,哥哥乘着以光速0. 98倍的速度飞行的宇宙飞船进行了5年宇宙旅行后回来了.这个5年是指地面上的5年,所以弟弟的年龄为25岁,可是哥哥的年龄在这段时间里只长了一岁,只有24岁,就这样,宇宙旅行后弟弟比哥哥反而大了1岁,请你用以上公式验证一下这个结论. -
科目: 来源: 题型:
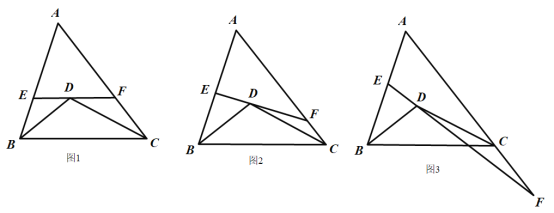
查看答案和解析>>【题目】已知,在△ABC中,BD平分∠ABC,CD平分∠ACB,BD,CD交于点D,EF过点D交AB于点E,交AC于点F.
(1)如图1,若EF∥BC,则∠BDE+∠CDF的度数为 (用含有∠A的代数式表示);
(2)当直线EF绕点D旋转到如图2所示的位置时,(1)中的结论是否成立?请说明理由;
(3)当直线EF绕点D旋转到如图3所示的位置时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请求出∠BDE,∠CDF与∠A之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

-
科目: 来源: 题型:
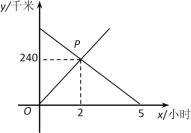
查看答案和解析>>【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?
相关试题

