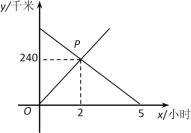
【题目】甲、乙二人驾车分别从A,B两地同时出发,相向而行.下图是二人离A地的距离y(千米)与所用时间x(小时)的关系.
(1)请说明交点P所表示的实际意义: ;
(2)试求出A,B两地之间的距离;
(3)甲从A地到达B地所需的时间为多少?
参考答案:
【答案】(1)出发2小时二人相遇,此时距离A地240千米;(2)400千米;(3)![]()
【解析】
(1)根据图象结合横纵坐标的意义即可得出P点的实际意义;
(2)先用待定系数法求出线段AB的解析式,然后令![]() 时,即可求出A,B两地之间的距离;
时,即可求出A,B两地之间的距离;
(3)根据A,B两地之间的距离和甲的速度即可求出时间.
解:(1)结合图象,可知P点的实际意义为出发2小时后甲、乙二人相遇,此时距离A地240千米
(2)如图,
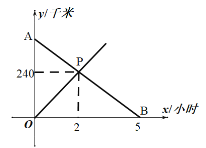
设线段AB的解析式为![]() ,
,
将![]() 代入解析式中得
代入解析式中得
![]() 解得
解得![]()
∴线段AB解析式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴A,B两地之间的距离为400千米.
(3)根据点P的坐标为![]() 得,甲的速度为
得,甲的速度为![]() ,
,
∴甲从A地到达B地所需的时间为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】城区某新建住宅小区计划购买并种植甲、乙两种树苗共300株.已知甲种树苗每株60元,乙种树苗每株90元.
(1)若购买树苗共用21000元,问甲、乙两种树苗应各买多少株?
(2)据统计,甲、乙两种树苗每株树苗对空气的净化指数分别为
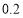 和
和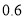 ,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90?
,问如何购买甲、乙两种树苗才能保证该小区的空气净化指数之和等于90? -
科目: 来源: 题型:
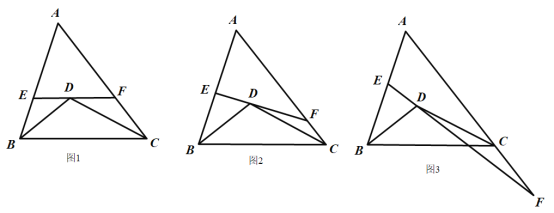
查看答案和解析>>【题目】已知,在△ABC中,BD平分∠ABC,CD平分∠ACB,BD,CD交于点D,EF过点D交AB于点E,交AC于点F.
(1)如图1,若EF∥BC,则∠BDE+∠CDF的度数为 (用含有∠A的代数式表示);
(2)当直线EF绕点D旋转到如图2所示的位置时,(1)中的结论是否成立?请说明理由;
(3)当直线EF绕点D旋转到如图3所示的位置时,(1)中的结论是否成立?若成立,请说明理由;若不成立,请求出∠BDE,∠CDF与∠A之间的关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y1=(m﹣2)x+2与正比例函数y2=2x图象相交于点A(2,n),一次函数y1=(m﹣2)x+2与x轴交于点B.
(1)求m、n的值;
(2)求△ABO的面积;
(3)观察图象,直接写出当x满足 时,y1>y2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,△ABC为等边三角形,点D,E为直线BC上两动点,且BD=CE. 点F,点E关于直线AC成轴对称,连接AE,顺次连接A,D,F.
(1)如图1,若点D,点E在边BC上,试判断△ADF的形状并说明理由;
(2)如图2,若点D,点E在边BC外,求证:
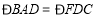 .
.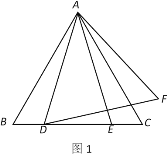
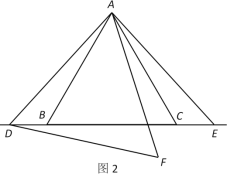
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣2x+4交x轴于点A,交y轴于点B,与反比例函数y=
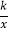 的图象有唯一的公共点C.
的图象有唯一的公共点C.(1)求k的值及C点坐标;
(2)直线l与直线y=﹣2x+4关于x轴对称,且与y轴交于点B',与双曲线y=
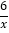 交于D、E两点,求△CDE的面积.
交于D、E两点,求△CDE的面积.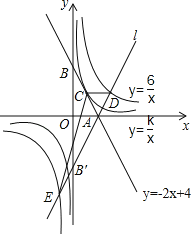
相关试题

