【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为6和8,对角线AC、BD相交于点O.则点P到矩形的两条对角线AC和BD的距离之和为_____.

参考答案:
【答案】![]()
【解析】首先连接OP,由矩形的两条边AB、BC的长分别为6和8,可求得OA=OD=5,△AOD的面积,然后由S△AOD=S△AOP+S△DOP=![]() OAPE+
OAPE+![]() ODPF求得答案.
ODPF求得答案.
连接OP,
∵矩形的两条边AB、BC的长分别为6和8,
∴S矩形ABCD=ABBC=48,OA=OC,OB=OD,AC=BD=![]() =10,
=10,
∴OA=OD=5,
∴S△ACD=![]() S矩形ABCD=24,
S矩形ABCD=24,
∴S△AOD=![]() S△ACD=12,
S△ACD=12,
∵S△AOD=S△AOP+S△DOP=![]() OAPE+
OAPE+![]() ODPF=
ODPF=![]() ×5×PE+
×5×PE+![]() ×5×PF=
×5×PF=![]() (PE+PF)=12,
(PE+PF)=12,
解得:PE+PF=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
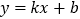 分别与
分别与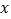 轴、
轴、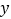 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数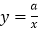 的图像相交于点
的图像相交于点 和点
和点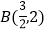 ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:①
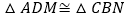 ;②
;②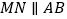 ;③四边形
;③四边形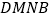 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④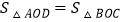 .其中正确的个数是( )个.
.其中正确的个数是( )个.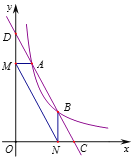
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:一个矩形的两邻边之比为
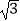 ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中,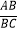 =
= 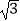 ,求∠AOD的度数;
,求∠AOD的度数; 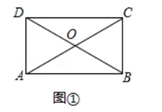
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB=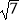 ,求矩形CDEF的面积;
,求矩形CDEF的面积; 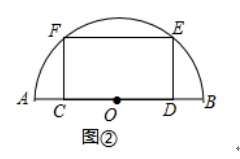
(3)在平面直角坐标系xOy中,⊙O的半径为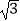 ,点Q的坐标为(q,2
,点Q的坐标为(q,2 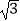 ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个
 的圆(∠AOB=90°),芳芳第一次在图1中画了一条线,将图1等分成2份,第二次又加了两条线,将图1等分成4份,第三次由加了四条线,将图1等分成8份,第四次又加了八条线,将图1等分成16份,如图2所示,则第n(n>1)次可将图1等分成_____份,当n=5时,图1中的每份的角度是_____(用度,分,秒表示)
的圆(∠AOB=90°),芳芳第一次在图1中画了一条线,将图1等分成2份,第二次又加了两条线,将图1等分成4份,第三次由加了四条线,将图1等分成8份,第四次又加了八条线,将图1等分成16份,如图2所示,则第n(n>1)次可将图1等分成_____份,当n=5时,图1中的每份的角度是_____(用度,分,秒表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②
 ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则 的最小值是1;⑤
的最小值是1;⑤ .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号) 
-
科目: 来源: 题型:
查看答案和解析>>【题目】自2014年12月28日北京公交地铁调价以来,人们的出行成本发生了较大的变化. 小林根据新闻,将地铁和公交车的票价绘制成了如下两个表格。(说明:表格中“6~12公里”指的是大于6公里,小于等于12公里,其他类似)

北京地铁新票价
里程范围
对应票价
0~6公里
3元
6~12公里
4元
12~22公里
5元
22~32公里
6元
32公里以上
每增加1元可再乘坐20公里
*持市政交通一卡通花费累计满一定金额后可打折

北京公交车新票价
里程范围
对应票价
0~10公里
2元
10~15公里
3元
15~20公里
4元
20公里以上
每增加1元可再乘坐5公里
*持市政交通一卡通刷卡,普通卡打5折,
学生卡打2.5折
根据以上信息回答下列问题:
小林办了一张市政交通一卡通学生卡,目前乘坐地铁没有折扣。
(1)如果小林全程乘坐地铁的里程为14公里,用他的学生卡需要刷卡交费________元;
(2)如果小林全程乘坐公交车的里程为16公里,用他的学生卡需要刷卡交________元;
(3)小林用他的学生卡乘坐一段地铁后换乘公交车,两者累计里程为12公里。已知他乘坐地铁平均每公里花费0.4元,乘坐公交车平均每公里花费0.25元,此次行程共花费4.5元。请问小林乘坐地铁和公交车的里程分别是多少公里?
相关试题

