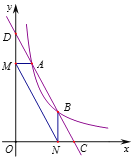
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
和点![]() ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④![]() .其中正确的个数是( )个.
.其中正确的个数是( )个.
A. 1 B. 2 C. 3 D. 4
参考答案:
【答案】C
【解析】根据待定系数法求出直线和反比例函数的解析式,得到CD点的坐标,由此求出DM、AM、CN、NB的长,然后根据SAS得到![]() ,然后根据M、N的求出MN的解析式,从而判断②,再根据①的结论和周长判断出③,最后根据三角形的面积判断④.
,然后根据M、N的求出MN的解析式,从而判断②,再根据①的结论和周长判断出③,最后根据三角形的面积判断④.
∵直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
和点![]()
∴一次函数的解析式为y=-2x+5,反比例函数的解析式为:y=![]()
∴C点为(![]() ,0),D点为(0,5)
,0),D点为(0,5)
∴DM=2,AM=1,CN=1,NB=2
∵AM⊥y轴,BN⊥x轴
∴![]() ,
,
故①正确;
由M(0,3),N(![]() ,0),求得MN的解析式为:y=-2x+3,
,0),求得MN的解析式为:y=-2x+3,
∴![]() ,故②正确;
,故②正确;
∵四边形![]() 的周长=BA+AD+DM+MN+NB=(BA+AD+MN)+DM+NB=(BA+AD+MN)+4
的周长=BA+AD+DM+MN+NB=(BA+AD+MN)+DM+NB=(BA+AD+MN)+4
四边形MNCA的周长=AM+AB+BC+MN+NC=(BA+BC+MN)+AM+NC=(BA+AD+MN)+2
∴四边形![]() 与四边形MNCA的周长不相等
与四边形MNCA的周长不相等
故③不正确;
由OD=5,AM=1,可得![]() =
=![]() ,由OC=
,由OC=![]() ,NB=2,可得
,NB=2,可得![]() =
=![]() =
=![]() ,可知
,可知![]() ,故④正确.
,故④正确.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(14分)盘锦红海滩景区门票价格80元/人,景区为吸引游客,对门票价格进行动态管理,非节假日打a折,节假日期间,10人以下(包括10人)不打折,10人以上超过10人的部分打b折,设游客为x人,门票费用为y元,非节假日门票费用
 (元)及节假日门票费用
(元)及节假日门票费用 (元)与游客x(人)之间的函数关系如图所示.
(元)与游客x(人)之间的函数关系如图所示.
(1)a= ,b= ;
(2)直接写出
 、
、 与x之间的函数关系式;
与x之间的函数关系式;(3)导游小王6月10日(非节假日)带A旅游团,6月20日(端午节)带B旅游团到红海滩景区旅游,两团共计50人,两次共付门票费用3040元,求A、B两个旅游团各多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小芳骑自行车从家出发到野外郊游.从家出发0.5小时到达甲地,游玩一段时间后按原速前往乙地.小芳离家1小时20分钟后,妈妈驾车沿相同路线前往乙地,行驶10分钟时,恰好经过甲地.如图是她们距乙地的路程y(km)与小芳离家x(h)的函数图象.
(1)小芳骑车的速度为 km/h,点H的坐标为 .
(2)小芳从家出发多少小时后被妈妈追上?此时距家的的路程多远?

(3)相遇后,妈妈载上小芳和自行车同时到达乙地(彼此交流时间忽略不计),求小芳比预计时间早几分钟到达乙地?
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
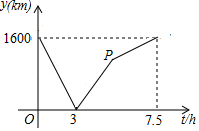
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:一个矩形的两邻边之比为
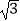 ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中,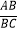 =
= 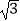 ,求∠AOD的度数;
,求∠AOD的度数; 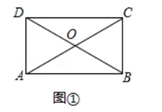
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB=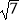 ,求矩形CDEF的面积;
,求矩形CDEF的面积; 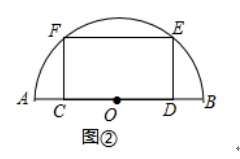
(3)在平面直角坐标系xOy中,⊙O的半径为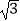 ,点Q的坐标为(q,2
,点Q的坐标为(q,2 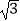 ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为6和8,对角线AC、BD相交于点O.则点P到矩形的两条对角线AC和BD的距离之和为_____.

相关试题

