【题目】定义:一个矩形的两邻边之比为 ![]() ,则称该矩形为“特比矩形”.
,则称该矩形为“特比矩形”.
(1)如图①,在“特比矩形”ABCD中, ![]() =
= ![]() ,求∠AOD的度数;
,求∠AOD的度数; 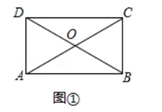
(2)如图②,特比矩形CDEF的边CD在半圆O的直径AB上,顶点E、F在半圆上,已知直径AB= ![]() ,求矩形CDEF的面积;
,求矩形CDEF的面积; 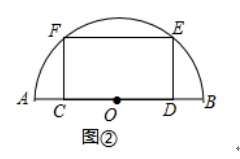
(3)在平面直角坐标系xOy中,⊙O的半径为 ![]() ,点Q的坐标为(q,2
,点Q的坐标为(q,2 ![]() ),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围.
),如果在⊙O上存在一点P,过点P作x轴的垂线与过点Q作y轴的垂线交于点M,过点P作y轴的垂线与过点Q作x轴的垂线交于点N,以点P、Q、M、N为顶点的矩形是“特比矩形”,请直接写出q的取值范围. 
参考答案:
【答案】
(1)解:如图①中,
∵四边形ABCD是矩形,
∴∠ABC=90°,OA=OC=OD=OB,
∴tan∠ACB= ![]() =
= ![]() ,
,
∴∠ACB=60°,∵OC=OB,
∴△OBC是等边三角形,
∴∠AOD=∠BOC=60°.
(2)解:如图②中,连接OE,设DE=a,则CD= ![]() a,
a,

∵CF=DE,OE=OF,∠FCO=∠EDO=90°,
∴Rt△FOC≌Rt△EDO,
∴OC=OD= ![]() a,
a,
在Rt△OED中,OE= ![]() ,
,
∵OE2=DE2+OD2,
∴ ![]() =a2+
=a2+ ![]() a2,
a2,
∴a=1(负根已经舍弃),
∴DE=1,CD= ![]() ,
,
∴矩形CDEF的面积=1× ![]() =
= ![]() .
.
(3)解:如图③中,

①当点P在x轴正半轴上,易知PM=2 ![]() ,
,
∵四边形PMQN是“特比矩形”,
∴MQ= ![]() PM=6,此时Q(
PM=6,此时Q( ![]() +6,2
+6,2 ![]() ),
),
当点P′在y轴的正半轴上时,P′M′= ![]() ,
,
∵四边形PMQN是“特比矩形”,
∴P′M′= ![]() M′Q′,
M′Q′,
∴M′Q′=1,
∴Q′(1,2 ![]() ),
),
根据对称性、观察图象可知:点Q的横坐标q的取值范围为1≤≤ ![]() +6或﹣
+6或﹣ ![]() ﹣6≤q≤﹣1.
﹣6≤q≤﹣1.
【解析】(1)由tan∠ACB= ![]() =
= ![]() ,推出∠ACB=60°,由OC=OB,推出△OBC是等边三角形即可解决问题.(2)如图②中,连接OE,设DE=a,则CD=
,推出∠ACB=60°,由OC=OB,推出△OBC是等边三角形即可解决问题.(2)如图②中,连接OE,设DE=a,则CD= ![]() a,由Rt△FOC≌Rt△EDO,推出OC=OD=
a,由Rt△FOC≌Rt△EDO,推出OC=OD= ![]() a,在Rt△OED中,OE=
a,在Rt△OED中,OE= ![]() ,根据OE2=DE2+OD2 , 列出方程即可解决问题.(3)取两个特殊点,求出点Q的坐标,再根据对称性即可解决问题.
,根据OE2=DE2+OD2 , 列出方程即可解决问题.(3)取两个特殊点,求出点Q的坐标,再根据对称性即可解决问题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两城由笔直的铁路连接,动车甲从A向B匀速前行,同时动车乙从B向A匀速前行,到达目的地时停止,其中动车乙速度较快,设甲乙两车相距y(km),甲行驶的时间为t(h),y关于t的函数图象如图所示.
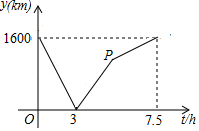
(1)填空:动车甲的速度为(km/h),动车乙的速度为(km/h);
(2)求图中点P的坐标,并解释该点坐标所表示的实际意义;
(3)两车何时相距1200km? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
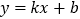 分别与
分别与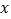 轴、
轴、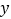 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数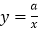 的图像相交于点
的图像相交于点 和点
和点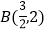 ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:①
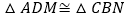 ;②
;②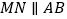 ;③四边形
;③四边形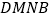 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④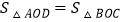 .其中正确的个数是( )个.
.其中正确的个数是( )个.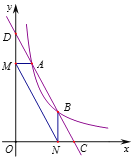
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P是矩形ABCD的边AD上的一个动点,矩形的两条边长AB、BC分别为6和8,对角线AC、BD相交于点O.则点P到矩形的两条对角线AC和BD的距离之和为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个
 的圆(∠AOB=90°),芳芳第一次在图1中画了一条线,将图1等分成2份,第二次又加了两条线,将图1等分成4份,第三次由加了四条线,将图1等分成8份,第四次又加了八条线,将图1等分成16份,如图2所示,则第n(n>1)次可将图1等分成_____份,当n=5时,图1中的每份的角度是_____(用度,分,秒表示)
的圆(∠AOB=90°),芳芳第一次在图1中画了一条线,将图1等分成2份,第二次又加了两条线,将图1等分成4份,第三次由加了四条线,将图1等分成8份,第四次又加了八条线,将图1等分成16份,如图2所示,则第n(n>1)次可将图1等分成_____份,当n=5时,图1中的每份的角度是_____(用度,分,秒表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B、C重合),过点C作CN垂直DM交AB于点N,连结OM、ON、MN.下列五个结论:①△CNB≌△DMC;②
 ;③ON⊥OM;④若AB=2,则
;③ON⊥OM;④若AB=2,则 的最小值是1;⑤
的最小值是1;⑤ .其中正确结论是_________.(只填番号)
.其中正确结论是_________.(只填番号) 
相关试题

