【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=![]() (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )

A. 1 B. ![]() C. 2
C. 2![]() ﹣
﹣![]() D.
D. ![]() ﹣1
﹣1
参考答案:
【答案】C
【解析】
由菱形ABCO,∠AOC=60°,由解直角三角形可以设A(m,![]() m),又点A在反比例函数的图像上,带入可以求出A的坐标,进而可以求出OA的长度,即OC可求。再根据菱形ABCO,∠AOC=60°,可知∠BOC=30°,可设E(n,0),则D(n,
m),又点A在反比例函数的图像上,带入可以求出A的坐标,进而可以求出OA的长度,即OC可求。再根据菱形ABCO,∠AOC=60°,可知∠BOC=30°,可设E(n,0),则D(n,![]() n),带入反比例函数的解析式可以求出E点坐标,于是CE=OC-OE,可求.
n),带入反比例函数的解析式可以求出E点坐标,于是CE=OC-OE,可求.
解:∵四边形ABCO为菱形,∠AOC=60°,
∴可设A(m,![]() m),
m),
又∵A点在反比例函数y=![]() 上,
上,
∴![]() m2=2
m2=2![]() ,得m=
,得m=![]() (由题意舍m=-
(由题意舍m=-![]() ),
),
∴A(![]() ,
,![]() ),OA=2
),OA=2![]() ,
,
∴OC=OA=2![]() ,
,
又∵四边形ABCO为菱形,∠AOC=60°,OB为四边形ABCO的对角线,
∴∠BOC=30°,可设D(n,![]() n),则E(n,0),
n),则E(n,0),
∵D在反比例函数y=![]() 上,
上,
∴![]() n2=2
n2=2![]() ,解得n=
,解得n=![]() (由题意舍n= -
(由题意舍n= -![]() ),
),
∴E(![]() ,0),
,0),
∴OE=![]() ,
,
则有CE=OC-OE=2![]() -
-![]() .
.
故答案选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】邮递员骑车从邮局出发,先向西骑行 2 km 到达 A 村,继续向西骑行 3 km 到达 B 村, 然后向东骑行 9 km 到达 C 村,最后回到邮局.
(1)以邮局为原点,以向东方向为正方向,用 1 cm 表示 1 km 画数轴,并在该数轴上表示 A,B,C 三个村庄的位置;
(2)C 村离 A 村有多远?
(3)邮递员一共骑行了多少千米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC中,CA=CB,∠ACB=120°,点E、F在AB上,且∠ECF=60°.
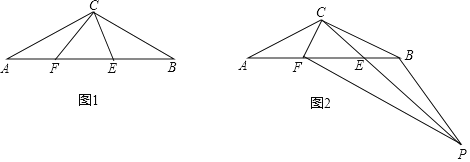
(1)①在图1中画出;点A关于直线CF的对称点G;②若EF=AF,求证:BE=EF;
(2)如图2,∠ABP=120°,射线BP交CE的延长线于点P,求证:PB+AF=PF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在平面直角坐标系中,点A在y轴正半轴上,点B、C分别在x轴的负半轴、正半轴上,且AB=AC,∠ACB=30°,OD⊥AB于点D.
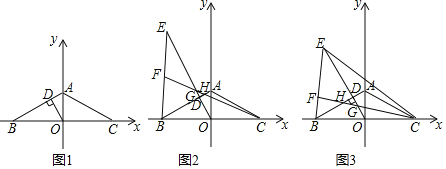
(1)求证:BD=3AD;
(2)如图2,点E在OD的延长线上,连接BE,在线段BE上取点F,连接CF分别交OE、AB于点G、H(点G、H、D互不重合),若FE=FG,求证:∠EBA﹣∠BCF的度数为定值;
(3)如图3,在(2)的条件下,连接EC,若C(4
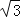 ,0),A(0,4),求S△ECG.
,0),A(0,4),求S△ECG. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
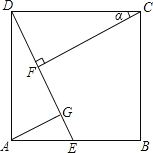
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
-
科目: 来源: 题型:
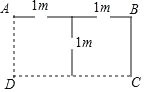
查看答案和解析>>【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽查了10名同学的期末成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,-3,+12,-7,-10,-3,-8,+1,0,+10.
(1)这10名同学中最高分是多少?最低分是多少?
(2)10名同学中,低于80分的所占的百分比是多少?
(3)10名同学的总成绩是多少?平均成绩是多少?
相关试题

