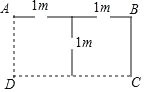
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.
参考答案:
【答案】(1)40-2x(2)15米或5米(3)不可能
【解析】
(1)直接由图可知AB=总长度+3-2x.
(2) 由题意得:(40﹣2x)x=150,解得即可.
(3)由题意判断(40﹣2x)x=210是否有解即可.
(1)∵中间共留三个 1 米的小门,
∴篱笆总长要增加 3 米,篱笆变为 40 米, 设篱笆 BC 长为 x 米,
∴AB=40﹣2x(米) 故答案为:40﹣2x.
(2)设篱笆 BC 长为 x 米. 由题意得:(40﹣2x)x=150解得:x=15,x=5
∴篱笆 BC 的长为:15 米或 5 米.
(3)不可能.
∵假设矩形鸡舍 ABCD 面积是 210 平方米, 由题意得:(40﹣2x)x=210,
整理得:x2﹣20x+105=0, 此方程中△<0,
∴方程无解.
故矩形鸡舍 ABCD 面积不可能达到 210 平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在平面直角坐标系中,点A在y轴正半轴上,点B、C分别在x轴的负半轴、正半轴上,且AB=AC,∠ACB=30°,OD⊥AB于点D.
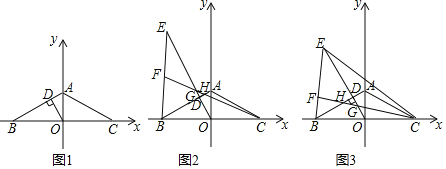
(1)求证:BD=3AD;
(2)如图2,点E在OD的延长线上,连接BE,在线段BE上取点F,连接CF分别交OE、AB于点G、H(点G、H、D互不重合),若FE=FG,求证:∠EBA﹣∠BCF的度数为定值;
(3)如图3,在(2)的条件下,连接EC,若C(4
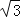 ,0),A(0,4),求S△ECG.
,0),A(0,4),求S△ECG. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,菱形ABCO的顶点O为坐标原点,边CO在x轴正半轴上,∠AOC=60°,反比例函数y=
 (x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
(x>0)的图象经过点A,交菱形对角线BO于点D,DE⊥x轴于点E,则CE长为( )
A. 1 B.
 C. 2
C. 2 ﹣
﹣ D.
D.  ﹣1
﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E在正方形ABCD的边AB上,连接DE,过点C作CF⊥DE于F,过点A作AG∥CF交DE于点G.
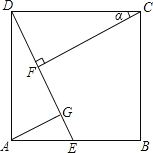
(1)求证:△DCF≌△ADG.
(2)若点E是AB的中点,设∠DCF=α,求sinα的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽查了10名同学的期末成绩,以80分为基准,超出的记为正数,不足的记为负数,记录的结果如下:+8,-3,+12,-7,-10,-3,-8,+1,0,+10.
(1)这10名同学中最高分是多少?最低分是多少?
(2)10名同学中,低于80分的所占的百分比是多少?
(3)10名同学的总成绩是多少?平均成绩是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一个点从数轴上的原点开始,先向右移动2个单位长度,再向左移动5个单位长度,可以看到终点表示是-3,已知A、B是数轴上的点,请参照下图并思考,完成下列各题.
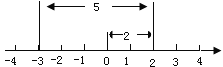
(1)如果点A表示的数-1,将点A向右移动4个单位长度,那么终点B表示的数是____.A、B两点间的距离是__________.
(2)如果点A表示的数2,将点A向左移动6个单位长度,再向右移动3个单位长度,那么终点B表示的数是____.A、B两点间的距离是____.
(3)如果点A表示的数m,将点A向左移动n个单位长度,再向左移动p个单位长度,那么请你猜想终点B表示的数是___.A、B两点间的距离是______.
-
科目: 来源: 题型:
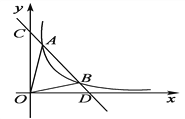
查看答案和解析>>【题目】如图,一次函数y=kx+b与反比例函数y=
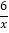 (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;
(2)根据图象直接写出kx+b-
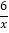 <0时x的取值范围;
<0时x的取值范围;(3)求△AOB的面积.
相关试题

