【题目】如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-![]() <0,求x的取值范围.
<0,求x的取值范围.

参考答案:
【答案】(1) y=-x-2;(2) 6;(3)-4<x<0.
【解析】试题分析:(1)因为A(-4,n)、B(2,-4)是一次函数y=kx+b的图象与反比例函数 y=![]() 的图象的两个交点,利用待定系数法,将点B(2,-4)代入反比例函数关系式求出k的值,再将A的横坐标代入,求出A的纵坐标,然后将A、B点的坐标代入一次函数y=kx+b,组成二元一次方程组,求出一次函数的关系式.
的图象的两个交点,利用待定系数法,将点B(2,-4)代入反比例函数关系式求出k的值,再将A的横坐标代入,求出A的纵坐标,然后将A、B点的坐标代入一次函数y=kx+b,组成二元一次方程组,求出一次函数的关系式.
(2)求出交点C的坐标,S△AOB=S△AOC+S△COB.
(3)根据图象,分别观察交点的那一侧能够使一次函数的值小于反比例函数的值,从而求得x的取值范围.
试题解析:(1)∵B(2,-4)在反比例函数y=![]() 的图象上,
的图象上,
∴m=-8,∴反比例函数的表达式为y=-![]() .
.
∵A(-4,n)在y=-![]() 的图象上,
的图象上,
∴n=2,∴A(-4,2).
∵y=kx+b经过A(-4,2)和B(2,-4),
∴![]() ,解得
,解得![]() ,
,
∴一次函数的表达式为y=-x-2.
(2)当y=-x-2=0时,解得x=-2.∴点C(-2,0),∴OC=2,
∴SΔAOB=SΔAOC+SΔCOB=![]() ×2×2+
×2×2+![]() ×2×4=6.
×2×4=6.
(3)根据函数的图象可知:x的取值范围是-4<x<0时,kx+b<![]() .
.
故答案为-4<x<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:方程
 ﹣
﹣ =
= ﹣
﹣ 的解是x=
的解是x=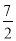 ,方程
,方程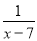 ﹣
﹣ =
= ﹣
﹣ 的解是x=
的解是x= ,试猜想:
,试猜想:(1)方程
 +
+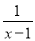 =
= +
+ 的解;
的解;(2)方程
 ﹣
﹣ =
= ﹣
﹣ 的解(a、b、c、d表示不同的数).
的解(a、b、c、d表示不同的数). -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)若a是(-4)2的平方根,b的一个平方根是2,求式子a+b的立方根;
(2)实数a,b互为相反数,c,d互为倒数,x的绝对值为
 ,求式子x2+(a+b+cd)x+
,求式子x2+(a+b+cd)x+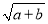 +
+ 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组:
(1)
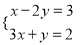 (2)
(2) 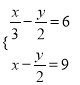
(3)
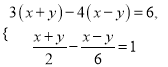 (4)
(4) 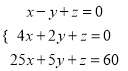
-
科目: 来源: 题型:
查看答案和解析>>【题目】电脑中有一种游戏——蜘蛛纸牌,开始游戏前有500分的基本分,游戏规则如下:①操作一次减x分;②每完成一列加y分.有一次小明在玩这种“蜘蛛纸牌”游戏时,随手用表格记录了两个时段的电脑显示:
第一时段
第二时段
完成列数
2
5
分数
634
898
操作次数
66
102
(1)通过列方程组,求x,y的值;
(2)如果小明最终完成此游戏(即完成10列),分数是1 182,问他一共操作了多少次?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 为
为 的直径,
的直径,  为弦
为弦 的中点,连接
的中点,连接 并延长交
并延长交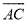 于点
于点 ,过点
,过点 作
作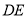 ∥
∥ ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 ,
,  .
.
(1)求证:
 是⊙
是⊙ 的切线;
的切线;(2)若
 时,
时,①求图中阴影部分的面积;
②以
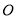 为原点,
为原点,  所在的直线为
所在的直线为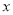 轴,直径
轴,直径 的垂直平分线为
的垂直平分线为 轴,建立如图所示的平面直角坐标系,试在线段
轴,建立如图所示的平面直角坐标系,试在线段 上求一点
上求一点 ,使得直线
,使得直线 把阴影部分的面积分成
把阴影部分的面积分成 的两部分.
的两部分. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 ABC的中线AD、BE相交于点F,下列结论正确的有 ( )
ABC的中线AD、BE相交于点F,下列结论正确的有 ( )①S△ABD=S△DCA;② S△AEF=S△BDF;③S四边形EFDC=2S△AEF;④S△ABC=3S△ABF
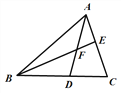
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

