【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
(1)若∠DCE=45°,则∠ACB的度数为;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE之间存在什么数量关系?并说明理由;
(4)当∠ACE<90°且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出∠ACE的值;若不存在,请说明理由. 
参考答案:
【答案】
(1)135°
(2)解:∵∠ACB=140°,∠ECB=90°
∴∠ACE=140°﹣90°=50°
∴∠DCE=90°﹣∠ACE=90°﹣50°=40°;
(3)解:猜想:∠ACB+∠DCE=180°
理由如下:∵∠ACE=90°﹣∠DCE
又∵∠ACB=∠ACE+90°
∴∠ACB=90°﹣∠DCE+90°=180°﹣∠DCE
即∠ACB+∠DCE=180°;
(4)解:15°、30°、45°;
理由:当CB∥AD时,∠ACE=30°;
当EB∥AC时,∠ACE=45°;
当BE∥AD时,∠ACE=15°.
【解析】解:∵∠DCE=45°,∠ACD=90° ∴∠ACE=45°
∵∠BCE=90°
∴∠ACB=90°+45°=135°
所以答案是:135°;
(1)根据∠DCE和∠ACD的度数,求得∠ACE的度数,再根据∠BCE求得∠ACB的度数;(2)根据∠BCE和∠ACB的度数,求得∠ACE的度数,再根据∠ACD求得∠DCE的度数;(3)根据∠ACE=90°﹣∠DCE以及∠ACB=∠ACE+90°,进行计算即可得出结论(4)分三种情况进行讨论:当CB∥AD时,当EB∥AC时,当BE∥AD时,分别求得∠ACE角度.
【考点精析】掌握余角和补角的特征和平行线的判定是解答本题的根本,需要知道互余、互补是指两个角的数量关系,与两个角的位置无关;同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,EF∥AD,AD∥BC,∠DAC=120°.

(1)若AB平分∠DAC,求∠ABC的度数.
(2)若∠ACF=20°,求∠BCF的度数.
(3)在(2)的条件下,若CE平分∠BCF,求∠CEF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形B.平行四边形C.正五边形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a|=﹣a,则下列a的取值不能使这个式子成立的是( )
A. 0 B. 1
C. ﹣2 D. a取任何负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,2,4,5,3的中位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.

(1)直接写出图中∠AOC的对顶角: , ∠EOB的邻补角:
(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=12cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
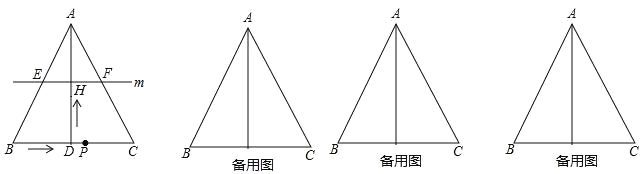
(1)连接DE、DF,当t为何值时,四边形AEDF为菱形?
(2)连接PE、PF,在整个运动过程中,△PEF的面积是否存在最大值?若存在,试求当△PEF的面积最大时,线段BP的长.
(3)是否存在某一时刻t,使点F在线段EP的中垂线上?若存在,请求出此时刻t的值;若不存在,请说明理由.
相关试题

