【题目】如图,EF∥AD,AD∥BC,∠DAC=120°. 
(1)若AB平分∠DAC,求∠ABC的度数.
(2)若∠ACF=20°,求∠BCF的度数.
(3)在(2)的条件下,若CE平分∠BCF,求∠CEF的度数.
参考答案:
【答案】
(1)解:∵AB平分∠DAC,∠DAC=120°,
∴∠DAB=60°,
又∵AD∥BC,
∴∠ABC=∠DAB=60°;
(2)解:∵AD∥BC,∠DAC=120°,
∴∠ACB=180°﹣120°=60°,
又∵∠ACF=20°,
∴∠BCF=60°﹣20°=40°;
(3)解:∵CE平分∠BCF,
∴∠BCE= ![]() ∠BCF=20°,
∠BCF=20°,
又∵EF∥AD,AD∥BC,
∴EF∥BC,
∴∠CEF=∠BCE=20°.
【解析】(1)根据角平分线的定义,可得∠DAB的度数,再根据平行线的性质,即可得出∠ABC的度数;(2)根据平行线的性质,即可得出∠ACB的度数,再根据角的和差关系,即可得到∠BCF的度数;(3)根据角平分线的定义,可得∠BCE的度数,再根据平行线的性质,即可得出∠CEF的度数.
【考点精析】认真审题,首先需要了解角的平分线(从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线),还要掌握平行线的性质(两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上到﹣1点的距离等于1个单位的点所表示的数是( )
A. 0 B. ﹣1 C. 1或﹣1 D. 0或﹣2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,在△ABC中,∠B<∠C,AD平分∠BAC,E的线段AD(除去端点A、D)上一动点,EF⊥BC于点F.
(1)若∠B=40°,∠DEF=10°,求∠C的度数.
(2)当E在AD上移动时,∠B、∠C、∠DEF之间存在怎样的等量关系?请写出这个等量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A(﹣3,﹣2),B(2,﹣2),C(3,1),D(﹣2,1)四个点.
(1)在图中描出A,B,C,D四个点,并顺次连接点A,B,C,D,A.
(2)直接写出线段AB,CD之间的关系.
(3)求四边形ABCD的面积.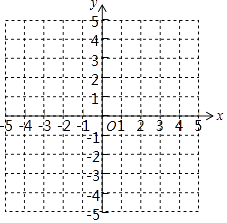
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等边三角形B.平行四边形C.正五边形D.圆
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果|a|=﹣a,则下列a的取值不能使这个式子成立的是( )
A. 0 B. 1
C. ﹣2 D. a取任何负数
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
(1)若∠DCE=45°,则∠ACB的度数为;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE之间存在什么数量关系?并说明理由;
(4)当∠ACE<90°且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出∠ACE的值;若不存在,请说明理由.
相关试题

