【题目】如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=12cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).
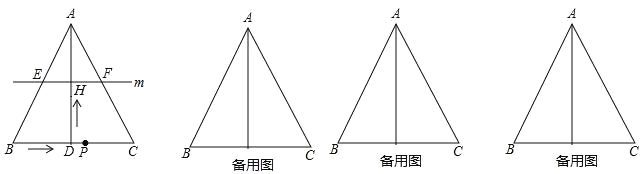
(1)连接DE、DF,当t为何值时,四边形AEDF为菱形?
(2)连接PE、PF,在整个运动过程中,△PEF的面积是否存在最大值?若存在,试求当△PEF的面积最大时,线段BP的长.
(3)是否存在某一时刻t,使点F在线段EP的中垂线上?若存在,请求出此时刻t的值;若不存在,请说明理由.
参考答案:
【答案】(1)当t=2s时,四边形AEDF为菱形;(2)BP=6cm;(3)存在某一时刻t,使点F在线段EP的中垂线上,t=![]() .
.
【解析】
试题分析:(1)根据四边形AEDF为菱形,则EF垂直平分AD,此时,DH=![]() AD=4cm,再根据直线m以每秒2cm的速度沿DA方向匀速平移,即可求得t=
AD=4cm,再根据直线m以每秒2cm的速度沿DA方向匀速平移,即可求得t=![]() =2(s);(2)先根据EF∥BC,得到△AEF∽△ABC,进而得出
=2(s);(2)先根据EF∥BC,得到△AEF∽△ABC,进而得出![]() ,据此求得EF=12﹣3t,再根据S△PEF=
,据此求得EF=12﹣3t,再根据S△PEF=![]() EFDH=
EFDH=![]() (12﹣3t)2t=﹣3t2+12t=﹣3(t﹣2)2+12(0<t≤4),求得当t=2秒时,S△PEF存在最大值,最大值为12cm2,最后计算线段BP的长;(3)若点F在线段EP的中垂线上,则FE=FP,过点F作FG⊥BC于G,则FG=HD=2t,FG∥AD,根据△FCG∽△ACD,得到
(12﹣3t)2t=﹣3t2+12t=﹣3(t﹣2)2+12(0<t≤4),求得当t=2秒时,S△PEF存在最大值,最大值为12cm2,最后计算线段BP的长;(3)若点F在线段EP的中垂线上,则FE=FP,过点F作FG⊥BC于G,则FG=HD=2t,FG∥AD,根据△FCG∽△ACD,得到![]() ,进而得到CG=
,进而得到CG=![]() t,PG=12﹣3t﹣
t,PG=12﹣3t﹣![]() t,最后在Rt△PFG中,根据勾股定理列出方程(12﹣3t﹣
t,最后在Rt△PFG中,根据勾股定理列出方程(12﹣3t﹣![]() t)2+(2t)2=(12﹣3t)2,即可求得t的值.
t)2+(2t)2=(12﹣3t)2,即可求得t的值.
试题解析:(1)如图1,若四边形AEDF为菱形,则EF垂直平分AD,
此时,DH=![]() AD=4cm,
AD=4cm,
又∵直线m以每秒2cm的速度沿DA方向匀速平移,
∴t=![]() =2(s),
=2(s),
此时,EF垂直平分AD,
∴AE=DE,AF=DF.
∵AB=AC,AD⊥BC于点D,
∴AD⊥BC,∠B=∠C.
∴EF∥BC,
∴∠AEF=∠B,∠AFE=∠C,
∴∠AEF=∠AFE,
∴AE=AF,
∴AE=AF=DE=DF,
即四边形AEDF为菱形,
故当t=2s时,四边形AEDF为菱形;
(2)如图2,∵直线m以每秒2cm的速度沿DA方向匀速平移,AD=8cm,
∴DH=2t,AH=8﹣2t,
∵EF∥BC,
∴△AEF∽△ABC,
∴![]() ,即
,即![]() .
.
解得EF=12﹣3t,
∴S△PEF=![]() EFDH=
EFDH=![]() (12﹣3t)2t=﹣3t2+12t=﹣3(t﹣2)2+12(0<t≤4),
(12﹣3t)2t=﹣3t2+12t=﹣3(t﹣2)2+12(0<t≤4),
∴当t=2秒时,S△PEF存在最大值,最大值为12cm2,
此时BP=3t=6cm;
(3)存在某一时刻t,使点F在线段EP的中垂线上.
∵AB=AC,AD⊥BC,BC=12cm,AD=8cm,
∴AB=AC=10cm,
若点F在线段EP的中垂线上,则FE=FP,
由(2)可得,EF=12﹣3t=PF,
如图3,过点F作FG⊥BC于G,则FG=HD=2t,FG∥AD,
∴△FCG∽△ACD,
∴![]() ,即
,即![]() ,
,
∴CG=![]() t,
t,
又∵BP=3t,BC=12cm,
∴PG=12﹣3t﹣![]() t,
t,
∴Rt△PFG中,(12﹣3t﹣![]() t)2+(2t)2=(12﹣3t)2,
t)2+(2t)2=(12﹣3t)2,
解得t1=![]() 或t2=0(舍去),
或t2=0(舍去),
∴当t=![]() 时,点F在线段EP的中垂线上.
时,点F在线段EP的中垂线上.



-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
(1)若∠DCE=45°,则∠ACB的度数为;
(2)若∠ACB=140°,求∠DCE的度数;
(3)猜想∠ACB与∠DCE之间存在什么数量关系?并说明理由;
(4)当∠ACE<90°且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出∠ACE的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数据1,2,4,5,3的中位数是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.

(1)直接写出图中∠AOC的对顶角: , ∠EOB的邻补角:
(2)若∠AOC=70°且∠BOE:∠EOD=2:3,求∠AOE的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,A(﹣2,1)、B(﹣4,﹣2)、C(﹣1,﹣3),△A′B′C′是△ABC平移之后得到的图象,并且C的对应点C′的坐标为(4,1)
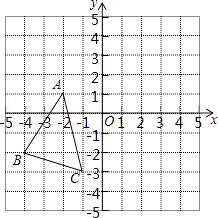
(1)A′、B′两点的坐标分别为A′、B′;
(2)作出△ABC平移之后的图形△A′B′C′;
(3)求△A′B′C′的面积. -
科目: 来源: 题型:
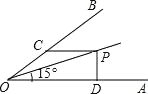
查看答案和解析>>【题目】如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD= .
-
科目: 来源: 题型:
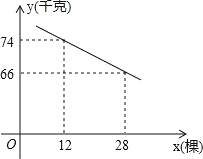
查看答案和解析>>【题目】某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果y(千克),增种果树x(棵),它们之间的函数关系如图所示.
(1)求y与x之间的函数关系式;
(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6750千克?
(3)当增种果树多少棵时,果园的总产量w(千克)最大?最大产量是多少?
相关试题

