【题目】已知,如图∠MON=30°,P为∠MON平分线上一点,PD⊥ON于D,PE∥ON,交OM于E,若OE=12cm,则PD长为 . 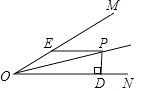
参考答案:
【答案】6cm
【解析】解:过点P作PC⊥OM, ∵PE∥ON,
∴∠EPO=∠POD,
∵OP是∠AOB的平分线,PD⊥ON,PC⊥OM,
∴∠COP=∠DOP,PC=PD,
∴∠EOP=∠EPO,
∴PE=OE=12cm,
∵∠MON=30°,
∴∠PEC=30°,
∴PC=6cm,
∴PD的长为6cm.
所以答案是:6cm.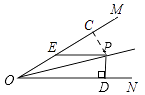
【考点精析】掌握平行线的性质和角平分线的性质定理是解答本题的根本,需要知道两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上.
-
科目: 来源: 题型:
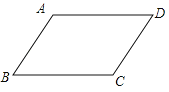
查看答案和解析>>【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
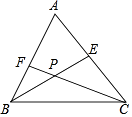
(1)若∠ABC=70°,∠ACB=50°,则∠BPC=°;
(2)求证:∠BPC=180°﹣ (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本-1,0,2,x,3,它们的平均数是2,则这个样本的方差s2 为( )
A.5B.3C.4D.6
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2﹣6x﹣5=0化为(x+m)2=n的形式,则m,n的值分别是( )
A.3和5
B.﹣3和5
C.﹣3和14
D.3和14 -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程组或不等式组.
(1)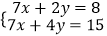
(2)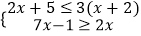 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD中,点C在AB的延长线上,连接DC.∠EDC=∠C,AD∥BE.
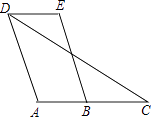
求证:∠A=∠E.
证明:∵∠EDC=∠C,
∴AB∥ . ()
∴ = . ()
∵AD∥BE,
∴∠A= . ()
∴∠A=∠E.(等量代换)
相关试题

