【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.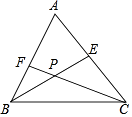
(1)若∠ABC=70°,∠ACB=50°,则∠BPC=°;
(2)求证:∠BPC=180°﹣ ![]() (∠ABC+∠ACB);
(∠ABC+∠ACB);
(3)若∠A=α,求∠BPC的度数.
参考答案:
【答案】
(1)120
(2)解:证明:∵∠ABC和∠ACB的平分线BE、CF相交于点P,
∴∠PBC= ![]() ∠ABC,∠PCB=
∠ABC,∠PCB= ![]() ∠ACB,
∠ACB,
∵∠BPC+∠PBC+∠PCB=180°,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣( ![]() ∠ABC+
∠ABC+ ![]() ∠ACB)=180°﹣
∠ACB)=180°﹣ ![]() (∠ABC+∠ACB),
(∠ABC+∠ACB),
∴∠BPC=180°﹣ ![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
(3)解:解:在△ABC中,∠A+∠ABC+∠ACB=180°,
∴∠ABC+∠ACB=180°﹣∠A,
∵由(2)可知:∠BPC=180°﹣ ![]() ∠ABC+∠ACB),
∠ABC+∠ACB),
∴∠BPC=180°﹣ ![]() (180°﹣∠A),
(180°﹣∠A),
∵∠A=α,
∴∠BPC=180°= ![]() (180°﹣α)=90°+
(180°﹣α)=90°+ ![]()
【解析】
①根据已知条件求出∠ABC+∠ACB,再根据角平分线的定义求出∠BPC+∠PCB,然后利用三角形的内角和等于180°列出计算.
②根据三角形的内角和和角平分线的定义即可得出结论.
③根据三角形的内角和和角平分线的定义即可.
【考点精析】根据题目的已知条件,利用三角形的内角和外角的相关知识可以得到问题的答案,需要掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一商店把某种品牌的羊毛衫按标价的八折出售,仍可获利20%,若该品牌的羊毛衫的进价每价是500元,则标价是每件元.
-
科目: 来源: 题型:
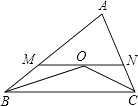
查看答案和解析>>【题目】△ABC中,BO平分∠ABC,CO平分∠ACB,MN过点O,交AB于M,交AC于N,且MN∥BC,若AB=12cm,AC=18cm,则△AMN周长为 .
-
科目: 来源: 题型:
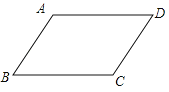
查看答案和解析>>【题目】如图,在ABCD中,已知AD>AB.
(1)实践与操作:作∠BAD的平分线交BC于点E,在AD上截取AF=AB,连接EF;(要求:尺规作图,保留作图痕迹,不写作法)
(2)猜想并证明:猜想四边形ABEF的形状,并给予证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个样本-1,0,2,x,3,它们的平均数是2,则这个样本的方差s2 为( )
A.5B.3C.4D.6
-
科目: 来源: 题型:
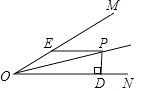
查看答案和解析>>【题目】已知,如图∠MON=30°,P为∠MON平分线上一点,PD⊥ON于D,PE∥ON,交OM于E,若OE=12cm,则PD长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】将方程x2﹣6x﹣5=0化为(x+m)2=n的形式,则m,n的值分别是( )
A.3和5
B.﹣3和5
C.﹣3和14
D.3和14
相关试题

