【题目】如图,已知反比例函数![]() 的图像与一次函数
的图像与一次函数![]() 的图像交于点
的图像交于点![]() ,点
,点![]() .
.
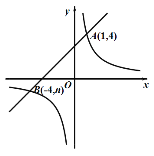
(1)求k和b的值;
(2)连接OA、OB,求![]() 的面积;
的面积;
(3)利用图像,直接写出![]() 时x的取值范围.
时x的取值范围.
参考答案:
【答案】(1)k=4;b=3;(2)7.5;(3)x>1或-4<x<0.
【解析】
(1)先根据反比例函数![]() 的图象过点A(1,4),可得k的值,再把A(1,4)代入一次函数的解析式可得b的值;
的图象过点A(1,4),可得k的值,再把A(1,4)代入一次函数的解析式可得b的值;
(2)把B(-4,n)代入![]() 得n=-1,连接OA、OB,分别求出直线与坐标轴的交点坐标,即可求出
得n=-1,连接OA、OB,分别求出直线与坐标轴的交点坐标,即可求出![]() 的面积;
的面积;
(3)根据题意,结合图象,找一次函数的图象在反比例函数图象上方的区域,易得答案.
(1)根据题意,反比例函数![]() 的图象过A(-1,4),
的图象过A(-1,4),
易得k=4;
则y=x+b的图象也过点(1、4);
代入解析式可得b=3;
∴y=x+3;
(2)∵B(-4,n)在直线y=x+3上,
∴n=-1,
∴B(-4,-1),
连接OA、OB,直线y=x+3与坐标轴分别交于C,D两点,如图,

对于y=x+3,令x=0,则y=3,即D(0,3);令y=0,则x=-3,即C(-3,0)
∴S△AOB=S△BOC+S△DOC+ S△DOA =![]() =7.5;
=7.5;
(3)根据图象,两个图象只有两个交点,
根据题意,找一次函数的图象在反比例函数图象上方的部分;
易得当x>1或-4<x<0时,有![]() ,
,
故当![]() 时,x的取值范围是x>1或-4<x<0.
时,x的取值范围是x>1或-4<x<0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
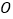 为坐标原点,点
为坐标原点,点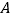 (0,1),点
(0,1),点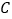 (1,0),正方形
(1,0),正方形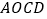 的两条对角线的交点为
的两条对角线的交点为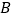 ,延长
,延长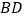 至点
至点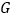 ,使
,使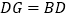 .延长
.延长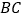 至点
至点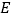 ,使
,使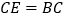 ,以
,以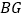 ,
,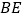 为邻边做正方形
为邻边做正方形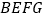 .
.(Ⅰ)如图①,求
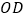 的长及
的长及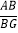 的值;
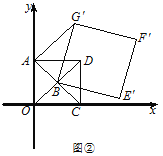
的值;(Ⅱ)如图②,正方形
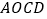 固定,将正方形
固定,将正方形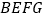 绕点
绕点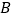 逆时针旋转,得正方形
逆时针旋转,得正方形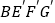 ,记旋转角为
,记旋转角为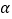 (0°<
(0°<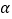 <360°),连接
<360°),连接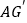 .
.①旋转过程中,当
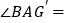 90°时,求
90°时,求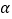 的大小;
的大小;②在旋转过程中,求
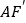 的长取最大值时,点
的长取最大值时,点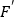 的坐标及此时
的坐标及此时 的大小(直接写出结果即可).
的大小(直接写出结果即可).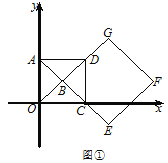
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)
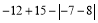
(2)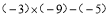
(3)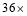 (
(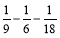 )
)
(4)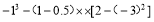
(5)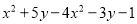
(6)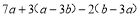
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F.
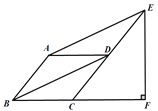
(1)求证:四边形ABCD是菱形;(2)若∠ABC=45°,BC=1,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“
 ”,向西记为“
”,向西记为“ ”,单位:千米):
”,单位:千米):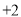 ,
,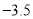 ,
,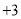 ,
,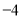 ,
,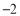 ,
,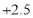 ,
,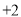
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走
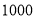 米耗油
米耗油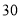 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升? -
科目: 来源: 题型:
查看答案和解析>>【题目】随着互联网的发展,农副产品也可以网上销售经过一段时间的精准帮扶,小张也建起了自家的网络商店(简称网店),他应用网店将种植的苹果和桃子销往全国各地.其中苹果每箱
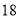 个
个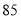 以上的
以上的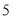 公斤左右包邮
公斤左右包邮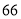 元;桃子每箱
元;桃子每箱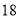 个
个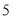 公斤左右包邮
公斤左右包邮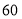 元.请你回答下列问题:
元.请你回答下列问题:(1)网购一箱苹果和一箱桃子共应支付___________元;
(2)某社区重阳节慰问困难居民,计划在这家网店购买
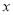 箱苹果和
箱苹果和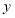 箱桃子,应支付的费用可表示为______________________元;
箱桃子,应支付的费用可表示为______________________元;(3)因为水果不耐贮存,小丽和两个同学合起来在这家网店购买了两箱苹果和一箱桃子,然后平均分配,小丽需支付多钱?她可以分到几个苹果和几个桃子?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在草莓上市的旺季,小颖和妈妈周末计划去草莓园采摘草莓.甲、乙两家草莓园生产的草莓品质相同,每千克售价均为
 元.甲草莓园的优惠方案是:游客进园需购买每人
元.甲草莓园的优惠方案是:游客进园需购买每人 元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过
元的门票,采摘的草莓按六折收费;乙草莓园的优惠方案是:游客进园不需购买门票,采摘的草莓超过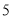 千克后,超过部分按五折收费.请你回答下列问题:
千克后,超过部分按五折收费.请你回答下列问题:(1)如果去乙草莓园采摘
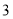 千克草莓,需支付多少元?
千克草莓,需支付多少元?(2)如果
 个人去甲草莓园采摘
个人去甲草莓园采摘 千克草莓,需支付多少元?
千克草莓,需支付多少元?(3)小颖和妈妈准备采摘
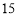 千克草莓送给朋友,哪家会更便宜?请说明理由.
千克草莓送给朋友,哪家会更便宜?请说明理由.
相关试题

