【题目】计算
(1)![]()
(2)![]()
(3)![]() (
(![]() )
)
(4)![]()
(5)![]()
(6)![]()
参考答案:
【答案】(1)-12;(2)32;(3)-4;(4)![]() ;(5)-3x2+2y-1;(6)16a-11b.
;(5)-3x2+2y-1;(6)16a-11b.
【解析】
(1)先化简绝对值,再根据有理数的加法法则计算即可;
(2)先算乘法,再算减法即可;
(3)利用分配律计算即可;
(4)先算乘方与括号内的运算,再算乘法,最后算加减即可;
(5)直接合并同类项即可;
(6)先去括号,再合并同类项即可.
(1)-12+15-|-7-8|
=-12+15-|-15|
=-12+15-15
=-12;
(2)(-3)×(-9)-(-5)
=27+5
=32;
(3)36×(![]() )
)
=4-6-2
=-4;
(4)-13-(1-0.5)×![]() ×[2-(-3)2]
×[2-(-3)2]
=-1-![]() ×
×![]() ×(2-9)
×(2-9)
=-1-![]() ×
×![]() ×(-7)
×(-7)
=-1+![]() ;
;
(5)x2+5y-4x2-3y-1
=-3x2+2y-1;
(6)7a+3(a-3b)-2(b-3a)
=7a+3a-9b-2b+6a
=16a-11b.
-
科目: 来源: 题型:
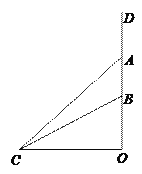
查看答案和解析>>【题目】如图,水渠边有一棵大木瓜树,树干
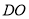 (不计粗细)上有两个木瓜
(不计粗细)上有两个木瓜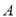 ,
,  (不计大小),树干垂直于地面,量得
(不计大小),树干垂直于地面,量得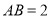 m,在水渠的对面与
m,在水渠的对面与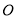 处于同一水平面的
处于同一水平面的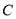 处测得木瓜
处测得木瓜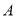 的仰角为45°、木瓜
的仰角为45°、木瓜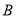 的仰角为30°.求
的仰角为30°.求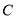 处到树干
处到树干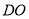 的距离
的距离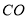 (结果精确到1m)(参考数据:
(结果精确到1m)(参考数据: 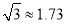 ,
, 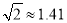 ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一位运动员推铅球,铅球运行时离地面的高度
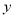 (米)是关于运行时间
(米)是关于运行时间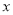 (秒)的二次函数.已知铅球刚出手时离地面的高度为
(秒)的二次函数.已知铅球刚出手时离地面的高度为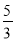 米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.
米;铅球出手后,经过4秒到达离地面3米的高度,经过10秒落到地面.如图建立平面直角坐标系.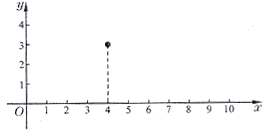
(Ⅰ)为了求这个二次函数的解析式,需要该二次函数图象上三个点的坐标.根据题意可知,该二次函数图象上三个点的坐标分别是____________________________;
(Ⅱ)求这个二次函数的解析式和自变量
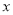 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,
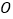 为坐标原点,点
为坐标原点,点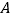 (0,1),点
(0,1),点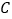 (1,0),正方形
(1,0),正方形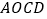 的两条对角线的交点为
的两条对角线的交点为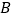 ,延长
,延长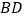 至点
至点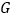 ,使
,使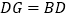 .延长
.延长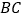 至点
至点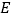 ,使
,使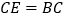 ,以
,以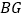 ,
,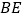 为邻边做正方形
为邻边做正方形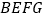 .
.(Ⅰ)如图①,求
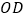 的长及
的长及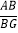 的值;
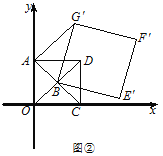
的值;(Ⅱ)如图②,正方形
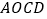 固定,将正方形
固定,将正方形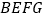 绕点
绕点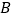 逆时针旋转,得正方形
逆时针旋转,得正方形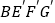 ,记旋转角为
,记旋转角为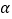 (0°<
(0°<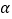 <360°),连接
<360°),连接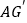 .
.①旋转过程中,当
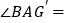 90°时,求
90°时,求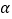 的大小;
的大小;②在旋转过程中,求
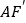 的长取最大值时,点
的长取最大值时,点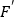 的坐标及此时
的坐标及此时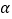 的大小(直接写出结果即可).
的大小(直接写出结果即可).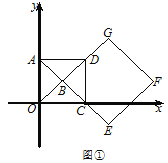
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线BD平分∠ABC,过点A作AE∥BD,交CD的延长线于点E,过点E作EF⊥BC,交BC的延长线于点F.
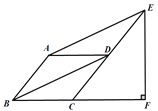
(1)求证:四边形ABCD是菱形;(2)若∠ABC=45°,BC=1,求EF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知反比例函数
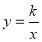 的图像与一次函数
的图像与一次函数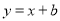 的图像交于点
的图像交于点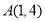 ,点
,点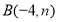 .
.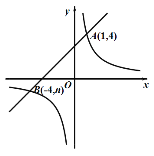
(1)求k和b的值;
(2)连接OA、OB,求
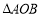 的面积;
的面积;(3)利用图像,直接写出
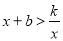 时x的取值范围.
时x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】快递员小王下午骑摩托车从总部出发,在一条东西走向的街道上来回收送包裹.他行驶的情况记录如下(向东记为“
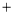 ”,向西记为“
”,向西记为“ ”,单位:千米):
”,单位:千米):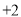 ,
,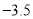 ,
,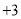 ,
,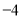 ,
,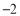 ,
,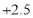 ,
,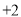
(1)小王最后是否回到了总部?
(2)小王离总部最远是多少米?在总部的什么方向?
(3)如果小王每走
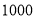 米耗油
米耗油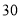 毫升,那么小王下午骑摩托车一共耗油多少毫升?
毫升,那么小王下午骑摩托车一共耗油多少毫升?
相关试题

