【题目】思考:填空,并探究规律
如图1,图2,OA∥EC,OB∥ED,∠AOB=30°,则图1中∠CED=_____°;图2中∠CED=_____°;用一句话概括你发现的规律_________________.
应用:已知∠AOB=80°,∠CED=x°,OA∥CE,OB∥ED,则x的值为_________(直接写出答案).

参考答案:
【答案】思考:30,150,两直线平行,同位角相等;应用:80或100.
【解析】
根据平行线性质定理,两直线平行,同位角相等,解答问题即可.
思考:∵OA∥EC,OB∥ED,∠AOB=30°
∴图1中∠CED=30°
∴图2中∠CED=150°
故答案为:30°;150°;两直线平行,同位角相等;
应用:∵∠AOB=80°,OA∥CE,OB∥ED,
∴图1中∠CED=80°
∴图2中∠CED=100°
∴答案为:80°或100°.
-
科目: 来源: 题型:
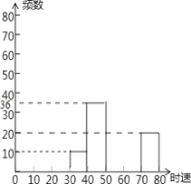
查看答案和解析>>【题目】某路段某时段用雷达测速仪随机监测了200辆汽车的时速,得到如下频数分布表(不完整):注:30﹣40为时速大于或等于30千米而小于40千米,其它类同.
数据段
频数
30~40
10
_______
36
50~60
80
60~70
_____
70~80
20
(1)请你把表中的数据填写完整;
(2)补全频数分布直方图;
(3)如果此路段该时间段经过的车有1000辆.估计约有多少辆车的时速大于或等于 60千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y=x+b,它的图象与两坐标轴所围成的图形的面积等于2.
(1)求b的值;
(2)若函数y=x+b的图象交y轴于正半轴,则当x取何值时,y的值是正数?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为 y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)a= ;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)若a≤x≤5,则当x为何值时,两车相距100km.

-
科目: 来源: 题型:
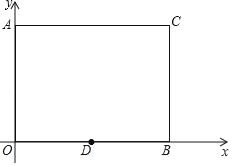
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(4,0),C为第一象限内一点,AC⊥y轴,BC⊥x轴,D坐标为(m,0)(0<m<4).
(1)若D为OB的中点,求直线DC的解析式;
(2)若△ACD为等腰三角形,求m的值;
(3)E为四边形OACB的某一边上一点.
①若E在边BC上,满足△AOD≌△DBE,求m的值;
②若使△EOD为等腰三角形的点E有且只有4个,直接写出符合条件的m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=﹣
 (x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(1)当m=2时,k= , b=;当m=﹣1时,k= , b=;
(2)根据(1)中的结果,用含m的代数式分别表示k与b,并证明你的结论;
(3)当正方形ABCD的顶点C落在抛物线的对称轴上时,求对应的抛物线的函数关系式;
(4)当正方形ABCD的顶点D落在抛物线上时,直接写出对应的直线y=kx+b的函数关系式.
相关试题

