【题目】如图,在平面直角坐标系中,直线y=kx+b分别与x轴、y轴交于A、B两点,过点B的抛物线y=﹣ ![]() (x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(x﹣2)2+m的顶点P在这条直线上,以AB为边向下方做正方形ABCD.
(1)当m=2时,k= , b=;当m=﹣1时,k= , b=;
(2)根据(1)中的结果,用含m的代数式分别表示k与b,并证明你的结论;
(3)当正方形ABCD的顶点C落在抛物线的对称轴上时,求对应的抛物线的函数关系式;
(4)当正方形ABCD的顶点D落在抛物线上时,直接写出对应的直线y=kx+b的函数关系式.
参考答案:
【答案】
(1)解: ![]() ;1;
;1;![]() ;﹣2
;﹣2
(2)
解:k= ![]() ,b=m﹣1.
,b=m﹣1.
证明:∵y=﹣ ![]() (x﹣2)2+m,
(x﹣2)2+m,
∴抛物线的顶点坐标为(2,m).
把x=0代入得:y=m﹣1.
∴b=m﹣1.
设直线AB的解析式为y=kx+m﹣1.
将x=2,y=m代入得:2k+m﹣1=m,解得k= ![]()
(3)
解:如图1所示,过点C作CE⊥y轴,垂足为E.

∵ABCD为正方形,
∴AB=BC,∠ABE+∠EBC=90°.
又∵∠ABO+∠BAO=90°,
∴∠BAO=∠EBC.
在△ABO和△BCE中  ,
,
∴△ABO≌△BCE.
∴EC=OB=2.
∴m﹣1=2.
∴m=3.
∴抛物线的解析式为y=﹣ ![]() (x﹣2)2+3
(x﹣2)2+3
(4)
解:如图2所示当点B在y轴的正半轴上时,过点D作DE⊥x轴与点E.

由(2)可知:直线AB的解析式为y= ![]() x+m﹣1.
x+m﹣1.
当x=0时,y=m﹣1,当y=0时,x=2﹣2m.
∴OA=2m﹣2,OB=m﹣1.
∵∠BAO+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAO=∠ADE.
在△ABO和△DAE中  ,
,
∴△ABO≌△DAE.
∴AE=OB=1﹣m,ED=AO=2m﹣2.
∴D(1﹣m,2﹣2m).
∵点D在抛物线上,
∴2﹣2m=﹣ ![]() (﹣m﹣1)2+m,解得m=9或m=1(舍去).
(﹣m﹣1)2+m,解得m=9或m=1(舍去).
∴直线的解析式为y= ![]() x+9.
x+9.
如图3所示:当点B在y轴的负半轴上时,

当x=0时,y=m﹣1,当y=0时,x=2﹣2m.
∴OA=2﹣2m,OB=1﹣m.
∵∠BAO+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAO=∠ADE.
在△ABO和△DAE中  ,
,
∴△ABO≌△DAE.
∴AE=OB,ED=AO.
∴D(3﹣3m,2m﹣2).
∵点D在抛物线上,
∴2m﹣2=﹣ ![]() (1﹣3m)2+m,解得m=﹣
(1﹣3m)2+m,解得m=﹣ ![]() 或m=1(舍去).
或m=1(舍去).
∴直线的解析式为y= ![]() x﹣
x﹣ ![]() .
.
综上所述,直线的解析式为y= ![]() x+9或y=
x+9或y= ![]() x﹣
x﹣ ![]()
【解析】解:(1)当m=2时,y=﹣ ![]() (x﹣2)2+2,
(x﹣2)2+2,
∴P(2,2).
把x=0代入得:y=1,
∴B(0,1).
设直线AB的解析式为y=kx+1,
将点P的坐标(2,2)代入得:2k+1=2,解得:k= ![]() .
.
∴k= ![]() ,b=1.
,b=1.
当m=﹣1时,y=﹣ ![]() (x﹣2)2﹣1.
(x﹣2)2﹣1.
∴P(2,﹣1).
把x=0代入得:y=﹣2,
∴B(0,﹣2).
设直线AB的解析式为y=kx﹣2,
将点P的坐标(2,﹣1)代入得:2k﹣2=﹣1,解得:k= ![]() .
.
∴k= ![]() ,b=﹣2.
,b=﹣2.
故答案为: ![]() ;1;
;1; ![]() ;﹣2.
;﹣2.
(1)将m的值代入可求得点P的坐标,将x=0代入求得y的值,从而可得到点B的坐标,然后利用待定系数法可求得直线AB的解析式;(2)由函数解析式得到点P的坐标,将x=0代入可求得y的值,从而得到点B的坐标,然后利用待定系数法求得AB的解析式,从而得到k、b的值;(3)过点C作CE⊥y轴,垂足为E.然后证明△ABO≌△BCE,从而可得到点B的坐标,然后由点B的坐标可求得点m的值;(4)当点B在y轴的正半轴上时,过点D作DE⊥x轴与点E.然后证明△ABO≌△DAE,从而可得到点D的坐标,然后将点D的坐标代入函数解析式可求得m的值,从而得到直线AB的解析式;当点B在y轴的负半轴上时,证明△ABO≌△DAE,从而可得到点D的坐标,然后将点D的坐标代入函数解析式可求得m的值,从而得到直线AB的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】思考:填空,并探究规律
如图1,图2,OA∥EC,OB∥ED,∠AOB=30°,则图1中∠CED=_____°;图2中∠CED=_____°;用一句话概括你发现的规律_________________.
应用:已知∠AOB=80°,∠CED=x°,OA∥CE,OB∥ED,则x的值为_________(直接写出答案).

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲,乙两车与B地的路程分别为 y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)a= ;
(2)求乙车与甲车相遇后y乙与x的函数解析式,并写出自变量x的取值范围;
(3)若a≤x≤5,则当x为何值时,两车相距100km.

-
科目: 来源: 题型:
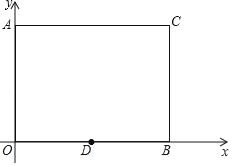
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,3),点B的坐标为(4,0),C为第一象限内一点,AC⊥y轴,BC⊥x轴,D坐标为(m,0)(0<m<4).
(1)若D为OB的中点,求直线DC的解析式;
(2)若△ACD为等腰三角形,求m的值;
(3)E为四边形OACB的某一边上一点.
①若E在边BC上,满足△AOD≌△DBE,求m的值;
②若使△EOD为等腰三角形的点E有且只有4个,直接写出符合条件的m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三角形ABC(记作△ABC)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是A(﹣2,1),B(﹣3,﹣2),C(1,﹣2),先将△ABC向上平移3个单位长度,再向右平移2个单位长度,得到A1B1C1.
(1)在图中画出△A1B1C1;
(2)点A1,B1,C1的坐标分别为 、 、 ;
(3)若y轴有一点P,使△PBC与△ABC面积相等,求出P点的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:点E、点G分别在直线AB、直线CD上,点F在两直线外,连接EF、FG

(1)如图1,AB∥CD,求证:∠AEF+∠FGC=∠EFG;
(2)若直线AB与直线CD不平行,连接EG,且EG同时平分∠BEF和∠FGD.
①如图2,请探究∠AEF、∠FGC、∠EFG之间的数量关系?并说明理由;
②如图3,∠AEF比∠FGC的3倍多10°,∠FGC是∠EFG的
 ,则∠EFG=______°(直接写出答案).
,则∠EFG=______°(直接写出答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机经销商计划同时购进一批甲、乙两种型号手机,若购进2部甲型号手机和5部乙型号手机,共需资金6000元;若购进3部甲型号手机和2部乙型号手机,共需资金4600元.
(1)求甲、乙型号手机每部进价多少元?
(2)为了提高利润,该店计划购进甲、乙型号手机销售,预计用不多于1.8万元且不少于1.76万元的资金购进这两种手机共20部,请问有几种进货方案?
(3)若甲型号手机的售价为1500元,乙型号手机的售价为1400元,为了促销,公司决定每售出一部乙型号手机,返还顾客现金a元;而甲型号手机售价不变,要使(2)中所有方案获利相同,求a的值.
相关试题

