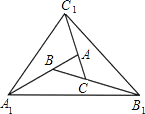
【题目】如图,对面积为1的△ABC逐次进行以下操作:第一次操作,分别延长AB、BC、CA至点A1、B1、C1,使得A1B=2AB,B1C=2BC,C1A=2CA,顺次连接A1、B1、C1得到△A1B1C1,记其面积为S1;第二次操作,分别延长A1B1、B1C1、C1A1至点A2、B2、C2,使得A2B1=2A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连按A2、B2、C2,得到△A2B2C2,记其面积为S2;按此规律继续下去,可得到△A2019B2019C2019,则其面积S2019=_____.
参考答案:
【答案】192019
【解析】
首先根据题意,求得![]() =2
=2![]() ,同理求得
,同理求得![]() =19
=19![]() ,则可求得面积S1的值;根据题意发现规律:Sn=19nS△ABC即可求得答案.
,则可求得面积S1的值;根据题意发现规律:Sn=19nS△ABC即可求得答案.
解:连接BC1,
∵C1A=2CA,
∴![]() =2S△ABC,
=2S△ABC,
同理:![]() =2
=2![]() =4S△ABC,
=4S△ABC,
∴![]() =6S△ABC,
=6S△ABC,
同理:![]() =
=![]() =6S△ABC,
=6S△ABC,
∴![]() =19S△ABC,
=19S△ABC,
即S1=19S△ABC,
∵S△ABC=1,
∴S1=19;
同理:S2=19S1=192S△ABC,S3=193S△ABC,
∴S2019=192019S△ABC=192019.
故答案是:192019.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,∠A=36°,分别以A和B为圆心,大于
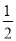 AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )
AB的长为半径作弧,两弧相交于M,N两点,作直线MN分别交AB、AC于点F、D,作DE⊥BC于E.有下面三个结论:①BD平分∠ABC;②DE=DF;③BC+CD=2AF;其中,正确的结论的个数是( )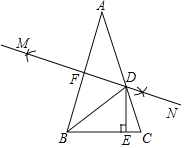
A.3B.2C.1D.0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,四边形
 为菱形,点
为菱形,点 ,
, 的坐标分别为
的坐标分别为 、
、 ,动点
,动点 从点
从点 出发,以每秒
出发,以每秒 个单位的速度沿
个单位的速度沿 向终点
向终点 运动,连接
运动,连接 并延长交
并延长交 于点
于点 ,过点
,过点 作
作 ,交
,交 于点
于点 ,连接
,连接 ,当动点
,当动点 运动了
运动了 秒时.
秒时.(1)
 点的坐标为________,
点的坐标为________, 点的坐标为________(用含
点的坐标为________(用含 的代数式表示);
的代数式表示);(2)记
 的面积为
的面积为 ,求
,求 与
与 的函数关系式
的函数关系式 ,并求出当
,并求出当 取何值时,
取何值时, 有最大值,最大值是多少?
有最大值,最大值是多少?(2)在
 出发的同时,有一动点
出发的同时,有一动点 从
从 点开始在线段
点开始在线段 上以每秒
上以每秒 个单位长度的速度向点
个单位长度的速度向点 移动,试求当
移动,试求当 为何值时,
为何值时, 与
与 相似.
相似.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市长途客运站每天6:30—7:30开往某县的三辆班车票价相同,但车的舒适程度不同.小张和小王因事需在这一时段乘车去该县,但不知道三辆车开来的顺序,两人采用不同的乘车方案:小张无论如何决定乘坐开来的第一辆车,而小王则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况.若第二辆车的状况比第一辆车好,他就上第二辆车;若第二辆车不如第一辆车,他就上第三辆车.若按这三辆车的舒适程度分为优、中、差三等,请你思考并回答下列问题:
(1)三辆车按出现的先后顺序共有哪几种可能?
(2)请列表分析哪种方案乘坐优等车的可能性大?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次促销活动中,某商场为了吸引顾客,设立了一个可以自由转动的转盘(如图,转盘被平均分成
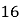 份),并规定:顾客每购买
份),并规定:顾客每购买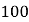 元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得
元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得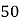 元、
元、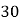 元、
元、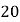 元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券
元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券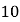 元.
元.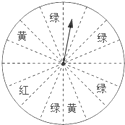
(1)求每转动一次转盘所获购物券金额的平均数;
(2)如果你在该商场消费
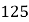 元,你会选择转转盘还是直接获得购物券?说明理由.
元,你会选择转转盘还是直接获得购物券?说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为吸引顾客,设立了一个可以自由转动的转盘,并规定每购买
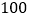 元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得
元商品可以获得一次转动转盘的机会,如果转盘停止转动时,指针正好落在红、绿、黄区域,那么顾客可以分别获得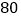 元、
元、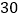 元、
元、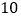 元购物券,如果不愿转动转盘,那么可以直接获得
元购物券,如果不愿转动转盘,那么可以直接获得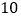 元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为
元购物券,设转盘停止转动时,指针正好落在红、绿、黄区域的概率依次为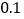 ,
,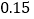 ,
,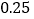 .
.(1)平均来说,每转动转盘
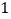 次所获得购物券的金额是多少?
次所获得购物券的金额是多少?(2)小明在家也做了一个同样的试验,转动转盘
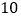 次后共得购物前
次后共得购物前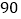 元,据此,小明认为,还是直接领取
元,据此,小明认为,还是直接领取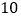 元购物券合算,你同意他的说法吗?
元购物券合算,你同意他的说法吗?
相关试题

