【题目】如图,四边形ABCD中,AC平分∠DAB,AC2=ABAD,∠ADC=90°,E为AB的中点.

(1)求证:△ADC∽△ACB;
(2)CE与AD有怎样的位置关系?试说明理由;
(3)若AD=4,AB=6,求![]() 的值.
的值.
参考答案:
【答案】(1)证明见解析;(2)CE∥AD,理由见解析;(3)![]() .
.
【解析】试题分析:(1)根据角平分线的定义得到∠DAC=∠CAB,根据相似三角形的判定定理证明;
(2)根据相似三角形的性质得到∠ACB=∠ADC=90°,根据直角三角形的性质得到CE=AE,根据等腰三角形的性质、平行线的判定定理证明;
(3)根据相似三角形的性质列出比例式,计算即可.
试题解析:(1)∵AC平分∠DAB,
∴∠DAC=∠CAB,
又∵AC2=ABAD,
∴AD:AC=AC:AB,
∴△ADC∽△ACB;
(2)CE∥AD,
理由:∵△ADC∽△ACB,
∴∠ACB=∠ADC=90°,
又∵E为AB的中点,
∴∠EAC=∠ECA,
∵∠DAC=∠CAE,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)∵AD=4,AB=6,CE=![]() AB=AE=3,
AB=AE=3,
∵CE∥AD,
∴∠FCE=∠DAC,∠CEF=∠ADF,
∴△CEF∽△ADF,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、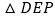 是两个全等的等腰直角三角形,
是两个全等的等腰直角三角形,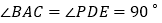 .
.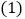 若将
若将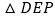 的顶点
的顶点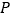 放在
放在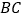 上(如图
上(如图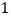 ),
),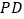 、
、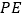 分别与
分别与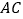 、
、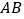 相交于点
相交于点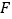 、
、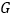 .求证:
.求证: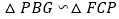 ;
;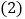 若使
若使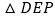 的顶点
的顶点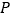 与顶点
与顶点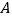 重合(如图
重合(如图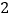 ),
),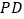 、
、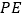 与
与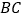 相交于点
相交于点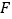 、
、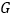 .试问
.试问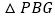 与
与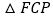 还相似吗?为什么?
还相似吗?为什么?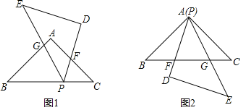
-
科目: 来源: 题型:
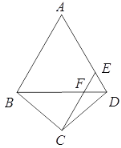
查看答案和解析>>【题目】如图,在四边形
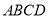 中,
中,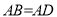 ,
,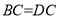 ,
,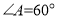 ,点
,点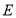 为
为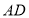 边上一点,连接
边上一点,连接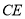 ,
,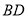 .
. 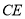 与
与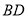 交于点
交于点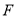 ,且
,且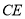 ∥
∥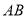 .
.
(1)求证:
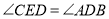 ;
;(2)若
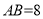 ,
,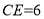 . 求
. 求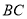 的长 .
的长 . -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后回答问题 .
已知
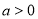 ,
,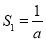 ,
,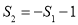 ,
, ,
,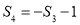 ,
,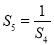 ,….,当
,….,当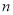 为大于1的奇数时,
为大于1的奇数时,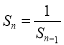 ;当
;当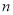 为大于1的偶数时,
为大于1的偶数时,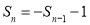 .
.(1)求
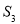 ;(用含
;(用含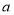 的代数式表示)
的代数式表示)(2)直接写出
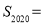 ;(用含
;(用含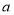 的代数式表示)
的代数式表示)(3)计算:
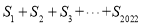 = .
= . -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若一个三角形中,其中有一个内角是另外一个内角的一半,则这样的三角形叫做“半角三角形”. 例如:等腰直角三角形就是“半角三角形”.在钝角三角形
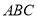 中,
中,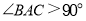 ,
,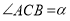 ,
,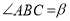 ,过点
,过点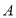 的直线
的直线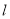 交
交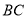 边于点
边于点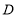 .点
.点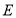 在直线
在直线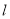 上,且
上,且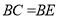 .
.(1)若
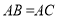 ,点
,点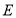 在
在 延长线上.
延长线上.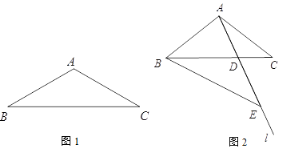
① 当
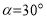 ,点
,点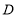 恰好为
恰好为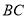 中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;
中点时,依据题意补全图1.请写出图中的一个“半角三角形”:_______;② 如图2,若
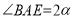 ,图中是否存在“半角三角形”(△
,图中是否存在“半角三角形”(△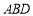 除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;
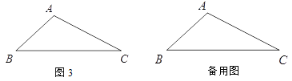
除外),若存在,请写出图中的“半角三角形”,并证明;若不存在,请说明理由;(2)如图3,若
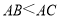 ,保持
,保持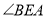 的度数与(1)中②的结论相同,请直接写出
的度数与(1)中②的结论相同,请直接写出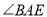 ,
,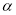 ,
,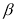 满足的数量关系:______.
满足的数量关系:______. -
科目: 来源: 题型:
查看答案和解析>>【题目】在
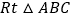 中,
中,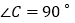 ,翻折
,翻折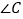 ,使点
,使点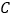 落在斜边
落在斜边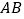 上某一点
上某一点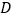 处,折痕为
处,折痕为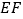 (点
(点 、
、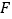 分别在边
分别在边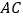 、
、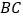 上)
上)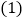 当
当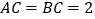 时,若
时,若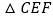 与
与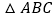 相似(如图
相似(如图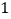 ),求
),求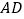 的长;
的长; 当点
当点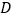 是
是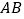 的中点时(如图
的中点时(如图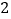 ),
),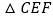 与
与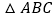 相似吗?请说明理由.
相似吗?请说明理由.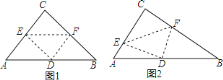
-
科目: 来源: 题型:
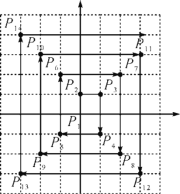
查看答案和解析>>【题目】如图,在平面直角坐标系中,每个最小方格的边长均为1个单位长度,P1,P2,P3,…均在格点上,其顺序按图中“→”方向排列,如:P1(0,0),P2(0,1),P3(1,1),P4(1,-1),P5(-1,-1),P6(-1,2),…,根据这个规律,点P2 019的坐标为_____
相关试题

