【题目】直线MN与直线PQ相交于O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.

(1)如图1,∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线,试求出∠AEB的度数.
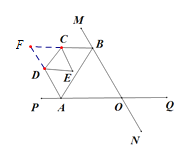
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)在(2)的条件下,在△CDE中,如果有一个角是另一个角的2倍,请直接写出∠DCE的度数.
参考答案:
【答案】(1) ∠AEB的度数为120°;(2) ∠CED的大小不发生变化,其值为60°;(3) ∠DCE的度数为40°或80°.
【解析】
(1)由∠POM=60°,∠BAO=70°,可求出∠ABO的值,根据AE、BE分别是∠BAO和∠ABO的角平分线,可得∠EAB和∠EBA的值,在△EAB中,根据三角形内角和即可得出∠AEB的大小;
(2)不发生变化,延长BC、AD交于点F,根据角平分线的定义以及三角形内角和可得∠F =90°-![]() ∠AOB,∠CED =90°-
∠AOB,∠CED =90°-![]() ∠F,即可得出∠CED的度数;
∠F,即可得出∠CED的度数;
(3)分三种情况求解即可.
解:(1)∵∠POM=60°,∠BAO=70°,
∴∠ABO=50°.
∵AE、BE分别是∠BAO和∠ABO的角平分线,
∴∠EAB=![]() ∠OAB=35°,∠EBA=
∠OAB=35°,∠EBA=![]() ∠OBA=25°,
∠OBA=25°,
∴∠AEB=180°-35°-25°=120°;
(2)不发生变化,理由如下:
如图,延长BC、AD交于点F,
∵点D、C分别是∠PAB和∠ABM的角平分线上的两点,
∴∠FAB=![]() ∠PAB=
∠PAB=![]() (180°-∠OAB),∠FBA=
(180°-∠OAB),∠FBA=![]() ∠MBA=
∠MBA=![]() (180°-∠OBA),
(180°-∠OBA),
∴∠FAB+∠FBA=![]() (180°-∠OAB)+
(180°-∠OAB)+![]() (180°-∠OBA)=
(180°-∠OBA)=![]() (180°+∠AOB)=90°+
(180°+∠AOB)=90°+![]() ∠AOB,
∠AOB,
∵∠AOB=60°,
∴∠F=180°-(∠FAB+∠FBA)=90°-![]() ∠AOB=60°,
∠AOB=60°,
同理可求∠CED =90°-![]() ∠F=60°;
∠F=60°;
(3)①当∠DCE=2∠E时,显然不符合题意;
②当∠DCE=2∠CDE时,∠DCE=![]() =80°;
=80°;
③当∠DCE=![]() ∠CDE时,∠DCE=
∠CDE时,∠DCE=![]() =40°,
=40°,
综上可知,∠DCE的度数40°或80°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
已知:PH∥AE,PK∥BC,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
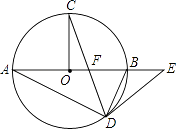
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌
国内品牌
进价(元/部)
4400
2000
售价(元/部)
5000
2500
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后解答后面两个问题.
解方程:|x+3|=2.
解:当x+3≥0时,原方程可化为x+3=2,解得x=-1;
当x+3<0时,原方程可化为x+3=-2,解得x=-5.
所以原方程的解是x=-1或x=-5.
(1)解方程:|3x-2|-4=0.
(2)已知关于x的方程|x-2|=b+1.
①若方程无解,则b的取值范围是 .
②若方程只有一个解,则b的值为 .
③若方程有两个解,则b的取值范围是 .
-
科目: 来源: 题型:
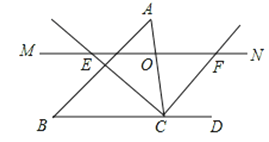
查看答案和解析>>【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由;
(2)若CE=8,CF=6,求OC的长
(3)连结AE,AF,当点O运动到何处时,四边形AECF是矩形?并说出你的理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】学校计划购买甲、乙两种图书作为“校园读书节”的奖品,已知甲种图书的单价比乙种图书的单价多10元,且购买3本甲种图书和2本乙种图书共需花费130元
(1)甲、乙两种图书的单价分别为多少元?
(2)学校计划购买这两种图书共50本,且投入总经费不超过1200元,则最多可以购买甲种图书多少本?
相关试题

