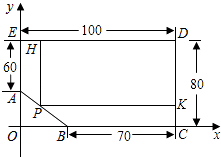
【题目】如图,为了绿化小区,某物业公司要在形如五边形ABCDE的草坪上建一个矩形花坛PKDH.
已知:PH∥AE,PK∥BC,DE=100米,EA=60米,BC=70米,CD=80米.以BC所在直线为x轴,AE所在直线为y轴,建立平面直角坐标系,坐标原点为O.
(1)求直线AB的解析式.
(2)若设点P的横坐标为x,矩形PKDH的面积为S,求S关于x的函数关系式.
参考答案:
【答案】
(1)解:如图所示,∵OE=80米,OC=ED=100米,AE=60米,BC=70米,
∴OA=20米,OB=30米,
即A、B的坐标为(0,20)、(30,0).
设直线AB的解析式为y=kx+b(k≠0),则 ![]() ,
,
解得, 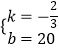 ,
,
则直线AB的解析式为y=﹣ ![]() x+20;
x+20;
(2)解:设点P的坐标为P(x,y).
∵点P在直线AB上,所以点P的坐标可以表示为(x,﹣ ![]() x+20),
x+20),
∴PK=100﹣x,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+ ![]() x,
x,
∴S=(100﹣x)(60+ ![]() x).
x).
【解析】根据题意容易求出A、B的坐标,利用待定系数法可以求出直线AB的解析式;(2)设点P的坐标为P(x,y),则PK=100﹣x,,PH=80﹣(﹣ ![]() x+20)=60+
x+20)=60+![]() x,,根据矩形的面积公式可以求得函数解析式。
x,,根据矩形的面积公式可以求得函数解析式。
【考点精析】关于本题考查的确定一次函数的表达式和矩形的性质,需要了解确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;矩形的四个角都是直角,矩形的对角线相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD,AF分别为△ABC的中线和高,BE为△ABD的角平分线.

(1)若∠BED=40°,∠BAD=25°,求∠BAF的大小;
(2)若△ABC的面积为40,BD=5,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】暑假期间,小刚一家乘车去离家380公里的某景区旅游,他们离家的距离y(km)与汽车行驶时间x(h)之间的三段函数图象如图.

(1)三段图像中,小刚行驶的速度最慢的是多少?
(2)求线段AB对应的函数表达式;
(3)小刚一家出发2.5小时时离目的地多远?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划用3 800元购进节能灯120只,这两种节能灯的进价、售价如下表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)求甲、乙两种节能灯各进多少只?
(2)全部售完120只节能灯后,该商场获利润多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB为直径,OC⊥AB,弦CD与OB交于点F,在AB的延长线上有一点E,且EF=ED.
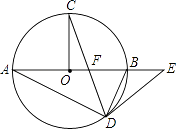
(1)求证:DE是⊙O的切线;
(2)若OF:OB=1:3,⊙O的半径R=3,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售国外、国内两种品牌的智能手机,这两种手机的进价和售价如下表所示:
国外品牌
国内品牌
进价(元/部)
4400
2000
售价(元/部)
5000
2500
该商场计划购进两种手机若干部,共需14.8万元,预计全部销售后可毛获利润共2.7万元.[毛利润=(售价﹣进价)×销售量]
(1)该商场计划购进国外品牌、国内品牌两种手机各多少部?
(2)通过市场调研,该商场决定在原计划的基础上,减少国外品牌手机的购进数量,增加国内品牌手机的购进数量.已知国内品牌手机增加的数量是国外品牌手机减少的数量的3倍,而且用于购进这两种手机的总资金不超过15.6万元,该商场应该怎样进货,使全部销售后获得的毛利润最大?并求出最大毛利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】直线MN与直线PQ相交于O,∠POM=60°,点A在射线OP上运动,点B在射线OM上运动.

(1)如图1,∠BAO=70°,已知AE、BE分别是∠BAO和∠ABO角的平分线,试求出∠AEB的度数.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)在(2)的条件下,在△CDE中,如果有一个角是另一个角的2倍,请直接写出∠DCE的度数.
相关试题

