Question

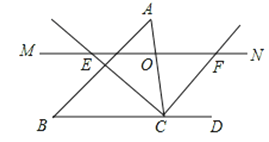
【题目】如图，△ABC中，点O是AC边上的一个动点，过点O作直线MN∥BC，交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．

（1）判断OE与OF的大小关系？并说明理由；

（2）若CE=8，CF=6，求OC的长

（3）连结AE，AF，当点O运动到何处时，四边形AECF是矩形？并说出你的理由．

Answer 1

【答案】（1）OE=OF；（2）5；（3）AC的中点时四边形AECF是矩形，理由见解析

【解析】

（1）根据CF平分∠ACD，且MN∥BD可证OF=OC，同理可证OE=OC，即可得OE=OF；
（2）根据三角形的内角和定理和等腰三角形的性质可求∠ECF=90°，根据勾股定理可求EF的长，根据直角三角形斜边上中线等于斜边的一半，可得OC的长；
（3）当点O在AC的中点时，由（1）知OE=OF，可证四边形AECF是平行四边形，再根据∠ECF=90°，可证四边形AECF是矩形．

解：（1）OE=OF，理由如下：

∵CF平分∠ACD，且MN∥BD
∴∠ACF=∠FCD=∠CFO
∴OF=OC
同理可证：OC=OE
∴OE=OF
（2）由（1）知：OF=OC=OE
∴∠OCF=∠OFC，∠OCE=∠OEC
∴∠OCF+∠OCE=∠OFC+∠OEC
而∠OCF+∠OCE+∠OFC+∠OEC=180°
∴∠ECF=∠OCF+∠OCE=90°
∴EF＝=＝10

∴OC＝EF＝5
（3）当点O移动到AC中点时，四边形AECF为矩形
理由如下：
∵当点O移动到AC中点时
∴OA=OC且OE=OF
∴四边形AECF为平行四边形
又∵∠ECF=90°
∴四边形AECF为矩形