Question

【题目】如图，在⊙O中，AB为直径，OC⊥AB，弦CD与OB交于点F，在AB的延长线上有一点E，且EF=ED．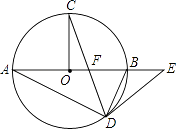

（1）求证：DE是⊙O的切线；
（2）若OF：OB=1：3，⊙O的半径R=3，求BE的长．

Answer 1

【答案】
（1）解：证明：连结OD，如图，

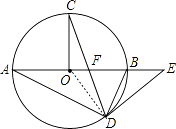
∵EF=ED，

∴∠EFD=∠EDF，

∵∠EFD=∠CFO，

∴∠CFO=∠EDF，

∵OC⊥OF，

∴∠OCF+∠CFO=90°，

而OC=OD，

∴∠OCF=∠ODF，

∴∠ODC+∠EDF=90°，即∠ODE=90°，

∴OD⊥DE，

∴DE是⊙O的切线；

（2）解：∵OF：OB=1：3，

∴OF=1，BF=2，

设BE=x，则DE=EF=x+2，

∵AB为直径，

∴∠ADB=90°，

∴∠ADO=∠BDE，

而∠ADO=∠A，

∴∠BDE=∠A，

而∠BED=∠DAE，

∴△EBD∽△EDA，

∴ = ，即 = ，

∴x=2，

∴BE=2．

【解析】（1）连结OD， 由等边对等角及对顶角相等得出∠CFO=∠EDF，由垂直定义得出∠OCF+∠CFO=90°，再由等边对等角得出∠OCF=∠ODF，进而得出∠ODC+∠EDF=90°，即∠ODE=90°，从而得出结论；（2）由OF：OB=1：3，得OF=1，BF=2，设BE=x，则DE=EF=x+2，进而判断出△EBD∽△EDA，再由相似三角形对应边成比例得出关于x的方程,求解即可。
【考点精析】本题主要考查了等腰三角形的性质和相似三角形的判定与性质的相关知识点，需要掌握等腰三角形的两个底角相等（简称：等边对等角）；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能正确解答此题．