【题目】已知抛物线![]() 与x轴交于A、B两点.
与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
参考答案:
【答案】(1)见解析(2)y=x2+2x﹣3;(3)![]()
【解析】
试题分析:(1)证明抛物线的对称轴<0即可证明抛物线的对称轴在y轴的左侧;
(2)根据题中已知条件求出m的值,进而求得抛物线的解析式;
(3)先设出C点坐标,根据的x1与x2关系求出m值,进而可求得△ABC的面积.
(1)证明:∵m>0,
∴x=﹣![]() =﹣
=﹣![]() <0,
<0,
∴抛物线的对称轴在y轴的左侧;
(2)解:设抛物线与x轴交点为A(x1,0),B(x2,0),
则x1+x2=﹣m<0,x1x2=﹣![]() m2<0,
m2<0,
∴x1与x2异号,
又∵![]() =
=![]() >0,
>0,
∴OA>OB,
由(1)知:抛物线的对称轴在y轴的左侧,
∴x1<0,x2>0,
∴OA=|x1|=﹣x1,
OB=x2,
代入![]() 得:
得:![]() =
=![]() ,
,
![]() =
=![]() ,
,
从而 ,
,
解得m=2,
经检验m=2是原方程的根,
∴抛物线的解析式为y=x2+2x﹣3;
(3)解:当x=0时,y=﹣![]() m2
m2
∴点C(0,﹣![]() m2),
m2),
∵△ABC是直角三角形,
∴AB2=AC2+BC2,
∴(x1﹣x2)2=x12+(﹣![]() m2)2+x22+(﹣
m2)2+x22+(﹣![]() m2)2
m2)2
∴﹣2x1x2=![]() m4
m4
∴﹣2(﹣![]() m2)=
m2)=![]() m4,
m4,
解得m=![]() ,
,
∴S△ABC=![]() ×ABOC=
×ABOC=![]() |x1﹣x2|
|x1﹣x2|![]() =
=![]() ×2m×
×2m×![]() m2=
m2=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在四边形ABCD中:①AB∥CD②AD∥BC③AB=CD④AD=BC,从以上选择两个条件使四边形ABCD为平行四边形的选法共有( )
A. 3种 B. 4种 C. 5种 D. 6种
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形具有而一般平行四边形不具有的性质是( )
A.对边相等 B.对角相等 C.对角线互相平分 D.对角线互相垂直
-
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按第一题计分.
A.一个多边形的每个内角都等于150°,则这个多边形是边形.
B.用计算器计算:sin15°32'(精确到0.01) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,AE⊥EF,∠DEA=30°.
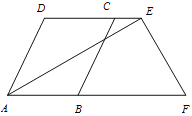
(1)求证:DC//AB.
(2)求∠AFE的大小
-
科目: 来源: 题型:
查看答案和解析>>【题目】将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和为( )
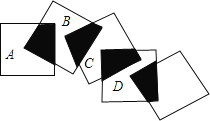
A.2cm2 B.4cm2 C.6cm2 D.8cm2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB
的某一边平行时,写出∠BAD的所有可能的值_____________

相关试题

