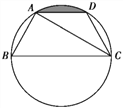
【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
参考答案:
【答案】(1)圆的半径为2;(2)![]() -
-![]()
【解析】试题分析:(1)已知AC平分∠BCD,由角平分线的定义可得∠ACD=∠ACB,
再由AD∥BC,即可得∠ACB=∠DAC=∠ACD,因∠ADC=120°,根据等腰三角形的性质和圆内接四边形互补可得∠ACB=∠DAC=∠ACD =30°,∠B=60°,根据圆周角定理的推论可得AB=AD=DC,且∠BAC=90°,即可BC为直径;设圆心为O,AB=x,则BC=2AB=2x,
由四边形ABCD的周长为10cm,可得x+x+x+2x=10,解得x=2,即可求得⊙O的半径为2;(2)设圆心为O,连接OA、OD,由(1)可知OA=OD=AD,可得△AOD为等边三角形,根据等边三角形的性质可得∠AOD=60°;因AD∥BC,可得![]() ,即可得
,即可得![]() .
.
试题解析:
(1)∵AC平分∠BCD,
∴∠ACD=∠ACB,
又∵AD∥BC,
∴∠ACB=∠DAC=∠ACD,
而∠ADC=120°,
∴∠ACB=∠DAC=∠ACD =30°,∠B=60°,
∴AB=AD=DC,且∠BAC=90°,
∴BC为直径,设圆心为O,AB=x,则BC=2AB=2x,
又∵四边形ABCD的周长为10cm,
∴x+x+x+2x=10,解得x=2,
即⊙O的半径为2.
(2)设圆心为O,连接OA、OD,
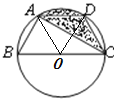
由(1)可知OA=OD=AD,
∴△AOD为等边三角形,
∴∠AOD=60°;
∵AD∥BC,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是⊙O的内接三角形,
是⊙O的内接三角形, 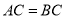 ,
, 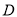 为⊙O中
为⊙O中 上一点,延长
上一点,延长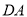 至点
至点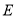 ,使
,使 .
.(1)求证:
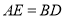 ;
;(2)若
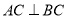 ,求证:AD+BD=
,求证:AD+BD=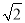 CD.
CD.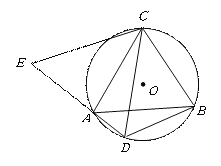
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形ABCD中,点A在x轴上,点B的坐标为(8,2),点D的坐标为(0,2),则菱形ABCD面积为( )
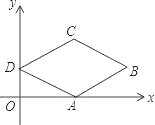
A. 8B. 16C. 24D. 32
-
科目: 来源: 题型:
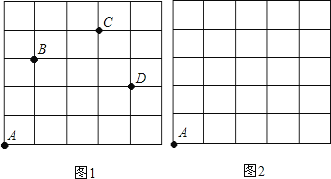
查看答案和解析>>【题目】如图,一只甲虫在5
 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为: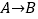 (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为: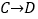 (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.(1)填空:
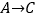 记为( , ),
记为( , ), 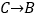 记为( , );
记为( , );(2)若甲虫的行走路线为:
 ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过点A的双曲线
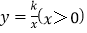 同时经过点B,且点A在点B的左侧,点A的横坐标为
同时经过点B,且点A在点B的左侧,点A的横坐标为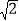 ,∠AOB=∠OBA=45°,则
,∠AOB=∠OBA=45°,则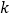 的值为_________.
的值为_________.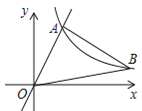
-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距90km,甲骑摩托车由A地出发,去B地办事,甲出发的同时,乙骑自行车同时由B地出发沿着同一条道路前往A地,甲办完事后原速返回A地,结果比乙早到0.5小时.甲、乙两人离A地距离y(km)与时间x(h)的函数关系图像如图所示.下列说法:①.a=3.5,b=4;② 甲走的全路程是90km;③乙的平均速度是22.5km/h;.④甲在B地办事停留了0.5小时.其中正确的说法有( )
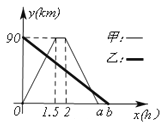
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

