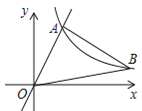
【题目】如图,在平面直角坐标系中,经过点A的双曲线![]() 同时经过点B,且点A在点B的左侧,点A的横坐标为
同时经过点B,且点A在点B的左侧,点A的横坐标为![]() ,∠AOB=∠OBA=45°,则
,∠AOB=∠OBA=45°,则![]() 的值为_________.
的值为_________.
参考答案:
【答案】1+![]()
【解析】分析:过A作AM⊥y轴于M,过B作BD垂直x轴于D,直线BD与AM交于点N,则OD=MN,DN=OM,∠AMO=∠BNA=90°,由等腰三角形的判定与性质得出OA=BA,∠OAB=90°,证出∠AOM=∠BAN,由AAS证明△AOM≌△BAN,得出AM=BN=![]() ,OM=AN=
,OM=AN=![]() ,求出B(
,求出B(![]() +
+![]() ,
,![]()
![]() ),得出方程(
),得出方程(![]() +
+![]() )(
)(![]()
![]() )=k,解方程即可.
)=k,解方程即可.
详解:过A作AM⊥y轴于M,过B作BD垂直x轴于D,直线BD与AM交于点N,如图所示: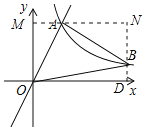
则OD=MN,DN=OM,∠AMO=∠BNA=90°,
∴∠AOM+∠OAM=90°,
∵∠AOB=∠OBA=45°,
∴OA=BA,∠OAB=90°,
∴∠OAM+∠BAN=90°,
∴∠AOM=∠BAN,
在△AOM和△BAN中,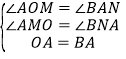 ,
,
∴△AOM≌△BAN(AAS),
∴AM=BN=![]() ,OM=AN=
,OM=AN=![]() ,
,
∴OD=![]() +
+![]() ,BD=
,BD=![]()
![]() ,
,
∴B(![]() +
+![]() ,
,![]()
![]() ),
),
∴双曲线y=![]() (x>0)同时经过点A和B,
(x>0)同时经过点A和B,
∴(![]() +
+![]() )(
)(![]()
![]() )=k,
)=k,
整理得:k2k4=0,
解得:k=1±![]() (负值舍去),
(负值舍去),
∴k=1+![]() ;
;
故答案为:1+![]() .
.
-
科目: 来源: 题型:
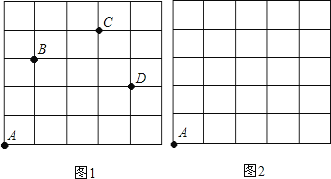
查看答案和解析>>【题目】如图,一只甲虫在5
 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为: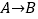 (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为: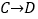 (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.(1)填空:
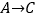 记为( , ),
记为( , ), 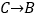 记为( , );
记为( , );(2)若甲虫的行走路线为:
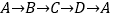 ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
-
科目: 来源: 题型:
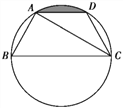
查看答案和解析>>【题目】如图,已知点A,B,C,D均在已知圆上,AD∥BC,CA平分∠BCD,∠ADC=120°,四边形ABCD的周长为10.
(1)求此圆的半径;
(2)求图中阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF,BE.
(1)求证:△AGE≌△BGF;
(2)试判断四边形AFBE的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】A、B两地相距90km,甲骑摩托车由A地出发,去B地办事,甲出发的同时,乙骑自行车同时由B地出发沿着同一条道路前往A地,甲办完事后原速返回A地,结果比乙早到0.5小时.甲、乙两人离A地距离y(km)与时间x(h)的函数关系图像如图所示.下列说法:①.a=3.5,b=4;② 甲走的全路程是90km;③乙的平均速度是22.5km/h;.④甲在B地办事停留了0.5小时.其中正确的说法有( )
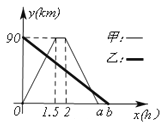
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】码头工人每天往一艘轮船上装载货物,装载速度y(吨/天)与装完货物所需时间x(天)之间的函数关系如图.

(1)求y与x之间的函数表达式;
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,装载完毕恰好用了8天时间,在(2)的条件下,至少需要增加多少名工人才能完成任务?
-
科目: 来源: 题型:
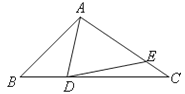
查看答案和解析>>【题目】如图,在△ABC中,∠B=45°,在BC边上取一点D,使CD=CA,点E在AC上,连接ED,若∠AED=45°,且CE=1,BD=2,则AD的长是 .
相关试题

