【题目】如图1,已知线段AB=16cm,点C为线段AB上的一个动点,点D、E分别是AC和BC的中点.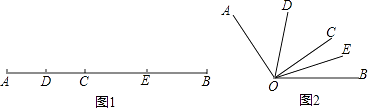
(1)若点C恰为AB的中点,求DE的长;
(2)若AC=6cm,求DE的长;
(3)试说明不论AC取何值(不超过16cm),DE的长不变;
(4)知识迁移:如图2,已知∠AOB=130°,过角的内部任一点C画射线OC,若OD、OE分别平分∠AOC和∠BOC,试说明∠DOE=65°与射线OC的位置无关.
参考答案:
【答案】
(1)解:∵点C恰为AB的中点,
∴AC=BC= ![]() AB=8cm,
AB=8cm,
∵点D、E分别是AC和BC的中点,
∴DC= ![]() AC=4cm,CE=
AC=4cm,CE= ![]() BC=4cm,
BC=4cm,
∴DE=8cm
(2)解:∵AB=16cm,AC=6cm,
∴BC=10cm,
由(1)得,DC= ![]() AC=3cm,CE=
AC=3cm,CE= ![]() CB=5cm,
CB=5cm,
∴DE=8cm
(3)解:∵点D、E分别是AC和BC的中点,
∴DC= ![]() AC,CE=
AC,CE= ![]() BC,
BC,
∴DE= ![]() (AC+BC)=
(AC+BC)= ![]() AB,
AB,
∴不论AC取何值(不超过16cm),DE的长不变
(4)解:∵OD、OE分别平分∠AOC和∠BOC,
∴∠DOC= ![]() ∠AOC,∠EOC=
∠AOC,∠EOC= ![]() ∠BOC,
∠BOC,
∴∠DOE=∠DOC+∠EOC= ![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)= ![]() ∠AOB=65°,
∠AOB=65°,
∴∠DOE=65°与射线OC的位置无关
【解析】(1)由点C恰为AB的中点,得到AC=BC的值,再由点D、E分别是AC和BC的中点,求出DE的值;(2)由(1)得,DC=![]() AC的值,CE=
AC的值,CE=![]() CB的值,得到DE的值;(3)由点D、E分别是AC和BC的中点,得到不论AC取何值(不超过16cm),DE的长不变;(4)由OD、OE分别平分∠AOC和∠BOC,根据角平分线定义,得到∠DOE=∠DOC+∠EOC=
CB的值,得到DE的值;(3)由点D、E分别是AC和BC的中点,得到不论AC取何值(不超过16cm),DE的长不变;(4)由OD、OE分别平分∠AOC和∠BOC,根据角平分线定义,得到∠DOE=∠DOC+∠EOC=![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB,得到∠DOE=65°与射线OC的位置无关.
∠AOB,得到∠DOE=65°与射线OC的位置无关.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
小明同学遇到下列问题:
解方程组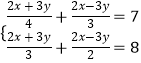 ,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
,他发现如果直接用代入消元法或加减消元法求解,运算量比较大,也容易出错.如果把方程组中的(2x+3y)看作一个数,把(2x﹣3y)看作一个数,通过换元,可以解决问题.以下是他的解题过程:
令m=2x+3y,n=2x﹣3y.
这时原方程组化为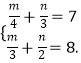 解得
解得 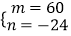
把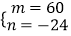 代入m=2x+3y,n=2x﹣3y.
代入m=2x+3y,n=2x﹣3y.
得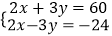 解得
解得 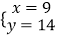
所以,原方程组的解为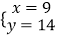
请你参考小明同学的做法,解决下面的问题:
(1)解方程组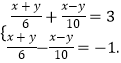
(2)若方程组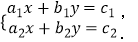 的解是
的解是 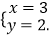 ,求方程组
,求方程组 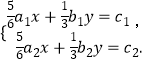 的解.
的解. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( )
A.“步行至十字路口,正好是红灯”是必然事件
B.一组数据的波动越大,方差越小
C.315期间,了解某种产品的质量问题,宜采用抽样调查数据
D.1,1,6,3,5,4,5的中位数是3
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°.求∠APC度数.
(1)小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得∠APC= .
问题迁移:如图3,AD∥BC,点P在射线OM上运动,∠ADP=∠α,∠BCP=∠β.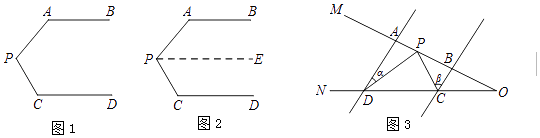
(2)当点P在A、B两点之间运动时,∠CPD、∠α、∠β之间有何数量关系?请说明理由.
(3)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∠CPD、∠α、∠β之间的数量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】以下问题,不适合用全面调查的是( )
A. 了解全班同学每周体育锻炼的时间
B. 调查七年级(1)班学生的某次数学考试成绩
C. 调查某班学生的身高
D. 了解全市中小学生每天的零花钱
-
科目: 来源: 题型:
查看答案和解析>>【题目】在大课间活动中,同学们积极参加体育锻炼.小丽在全校随机抽取一部分同学就“一分钟跳绳”进行测试,并以测试数据为样本绘制如图所示的部分频数分布直方图(从左到右依次分为六个小组,每小组含最小值,不含最大值)和扇形统计图,若“一分钟跳绳”次数不低于130次的成绩为优秀,全校共有1200名学生,根据图中提供的信息,下列说法不正确的是( )
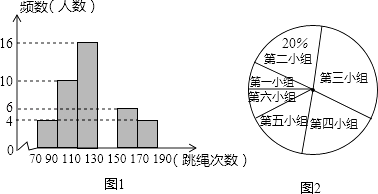
A.第四小组有10人
B.第五小组对应圆心角的度数为45°
C.本次抽样调查的样本容量为50
D.该校“一分钟跳绳”成绩优秀的人数约为480人 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
如图1,需要在A,B两地和公路l之间修地下管道,请你设计一种最节省材料的修建方案.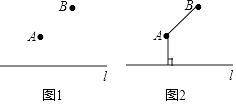
小军同学的作法如下:
①连接AB;
②过点A作AC⊥直线l于点C;
则折线段B﹣A﹣C为所求.
老师说:小军同学的方案是正确的.
请回答:该方案最节省材料的依据是 .
相关试题

