【题目】在等腰三角形ABCD中,AB=AC,分别在射线AB、CA上取点D、E,连结DE,过点E作EF∥AB交直线BC于点F,直线BC与DE所在直线交于点M.
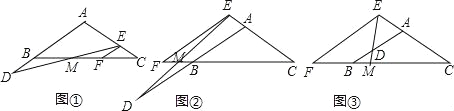
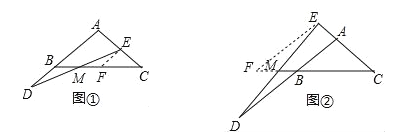
猜想:如图①,点D在边AB延长线上,点E在边AC上,且BD=CE,则线段BM、EM的大小关系为 .
探究:如图②,点D、E分别在边AB、CA延长线上,且BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:如图③,点D在边AB上(点D不与点A、B重合),点E在边CA的延长线上,其它条件不变,若BD=1,CE=4,DM=0.7,则线段DE的长为 .
参考答案:
【答案】猜想:DM=EM;探究:DM=EM;拓展:2.1.
【解析】
试题分析:(1)根据等腰三角形的性质和平行线的性质得到∠D=∠MEF,证明△BDM≌△FEM即可;
(2)根据等腰三角形的性质和平行线的性质得到∠D=∠MEF,证明△BDM≌△FEM即可;
(3)根据等腰三角形的性质和平行线的性质得到EF=CE由BD∥EF得![]() ,代入数据即可得到结论.
,代入数据即可得到结论.
试题解析:(1)猜想:DM=EM.
理由:∵AB=AC,
∴∠ABC=∠C,
∵EF∥AD,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
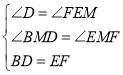 ,
,
∴△BDM≌△FEM,
∴DM=EM.
(2)结论DM=EM.
理由:∵AB=AC,
∴∠ABC=∠C,
∵EF∥AB,
∴∠EFC=∠ABC,
∴∠C=∠EFC,
∴EF=EC,
∵BD=EC,
∴DB=EF,
∵EF∥AB,
∴∠D=∠MEF,
在△BDM和△FEM中,
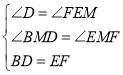 ,
,
∴△BDM≌△FEM,
∴DM=EM.
(3)∵EF∥AB,
∴∠F=∠ABC,
∵AB=AC,
∴∠ABC=∠C,
∴∠F=∠C,
∴EF=CE=4,
∵BD∥EF,
∴![]() ,
,
∴![]() ,
,
∴EM=2.8,
∴DE=EM-DM=2.1,
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆内接四边形ABCD的内角∠A:∠B:∠C=2:3:4,则∠D=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能够与正八边形平铺底面的正多边形是_______________.(请从正六边形、正方形、正三角形、正十边形中选择一种正多边形).
-
科目: 来源: 题型:
查看答案和解析>>【题目】长度为2cm、3cm、4cm、5cm的四条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程x2+2x+1=4较适宜的方法是( )
A. 实验法 B. 公式法 C. 因式分解法 D. 配方法
-
科目: 来源: 题型:
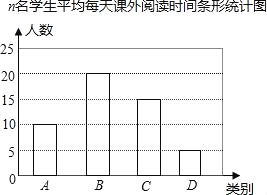
查看答案和解析>>【题目】课外阅读是提高学生素养的重要途径,某校团委为了解学生课外阅读情况,随机抽查了本校n名学生,统计它们平均每天课外阅读时间t(时),并根据时间t的长短分为A、B、C、D四类,(A)0<t<0.5,(B)0.5≤t<1,(C)1≤t<1.5,(D)t≥1.5,并根据抽查的人数绘制如下统计图.
(1)求n的值.
(2)四类中人数最多的是 (用A、B、C、D作答),选择该类的学生人数占被调查的学生人数的百分比为 .
(3)该校现有1300名学生,估计该校学生课外阅读时间不少于1小时的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/个)
售价(元/个)
电饭煲
200
250
电压锅
160
200
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
相关试题

