【题目】能够与正八边形平铺底面的正多边形是_______________.(请从正六边形、正方形、正三角形、正十边形中选择一种正多边形).
参考答案:
【答案】正方形
【解析】分析:分别求出每一个正多边形每一个内角的度数,然后根据密铺的条件得出答案.
详解:∵正八边形的内角为135°,正六边形的内角为120°,正方形的内角为90°,正三角形的内角为60°,正十边形的内角为144°,
∵135°×2+90°=360°, ∴选择正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形底边长为6cm,腰长为5cm,则它的周长为( ).
A.19
B.16
C.14
D.16或17 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形两边长分别为6cm和12cm,则底边长为( ),周长为( ).
A.6,30
B.16,25
C.14,30
D.12,30 -
科目: 来源: 题型:
查看答案和解析>>【题目】圆内接四边形ABCD的内角∠A:∠B:∠C=2:3:4,则∠D=__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】长度为2cm、3cm、4cm、5cm的四条线段,若以其中的三条线段为边构成三角形,可以构成不同的三角形共有( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
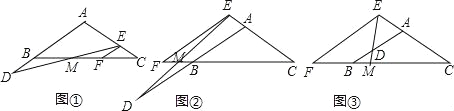
查看答案和解析>>【题目】在等腰三角形ABCD中,AB=AC,分别在射线AB、CA上取点D、E,连结DE,过点E作EF∥AB交直线BC于点F,直线BC与DE所在直线交于点M.
猜想:如图①,点D在边AB延长线上,点E在边AC上,且BD=CE,则线段BM、EM的大小关系为 .
探究:如图②,点D、E分别在边AB、CA延长线上,且BD=CE,判断线段DM、EM的大小关系,并加以证明.
拓展:如图③,点D在边AB上(点D不与点A、B重合),点E在边CA的延长线上,其它条件不变,若BD=1,CE=4,DM=0.7,则线段DE的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程x2+2x+1=4较适宜的方法是( )
A. 实验法 B. 公式法 C. 因式分解法 D. 配方法
相关试题

