Question

【题目】如图，在四边形ABCD中，AB=CD，BF=DE，AE⊥BD，CF⊥BD，垂足分别为E，F．

（1）求证：△ABE≌△CDF；

（2）若AC与BD交于点O，求证：AO=CO．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

试题分析：（1）由BF=DE，可得BE=DF，由AE⊥BD，CF⊥BD，可得∠AEB=∠CFD=90°，又由AB=CD，在直角三角形中利用HL即可证得：△ABE≌△CDF；

（2）由△ABE≌△CDF，即可得∠ABE=∠CDF，根据内错角相等，两直线平行，即可得AB∥CD，又由AB=CD，根据有一组对边平行且相等的四边形是平行四边形，即即可证得四边形ABCD是平行四边形，则可得AO=CO．

试题解析：（1）∵BF=DE，

∴BF-EF=DE-EF，

即BE=DF，

∵AE⊥BD，CF⊥BD，

∴∠AEB=∠CFD=90°，

∵AB=CD，

∴Rt△ABE≌Rt△CDF（HL）；

（2）连接AC，如图：

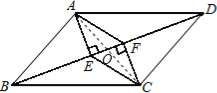
∵△ABE≌△CDF，

∴∠ABE=∠CDF，

∴AB∥CD，

∵AB=CD，

∴四边形ABCD是平行四边形，

∴AO=CO．

考点: 1.平行四边形的判定与性质；2.全等三角形的判定与性质.