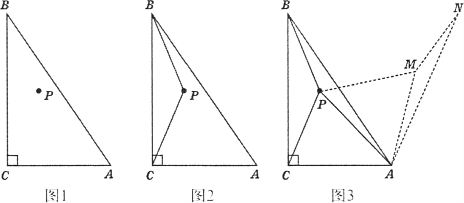
【题目】如图1,在△ABC中,∠ACB=90°,点P为ΔABC内一点.
(1)连接PB,PC,将ABCP沿射线CA方向平移,得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将ΔABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
参考答案:
【答案】(1)①补图见解析;②![]() ;(2)
;(2)![]()
【解析】试题分析:(1)根据作平移图形的方法作图即可;(2)证明四边形BCAD是矩形,得到CD=AB=6,由平移的性质得DE=BP=3,由BP⊥CE,BP∥DE得到△DEC是直角三角形,根据![]() 即可求出CE的长度;(3)当C、P、M、N四点共线时,PA+PB+PC最小,由旋转可得,△AMN≌△APB, PB=MN,易得△APM、△ABN都是等边三角形,所以PA=PM,则PA+PB+PC=PM+MN+PC=CN,所以BN=AB=6,∠BNA=60°,∠PAM=60°,根据∠CAN=∠CAB+∠BAN=120°,所以∠CBN=90°,在Rt△ABC中,求得
即可求出CE的长度;(3)当C、P、M、N四点共线时,PA+PB+PC最小,由旋转可得,△AMN≌△APB, PB=MN,易得△APM、△ABN都是等边三角形,所以PA=PM,则PA+PB+PC=PM+MN+PC=CN,所以BN=AB=6,∠BNA=60°,∠PAM=60°,根据∠CAN=∠CAB+∠BAN=120°,所以∠CBN=90°,在Rt△ABC中,求得![]() ,在Rt△BCN中,
,在Rt△BCN中, ![]() 即为所求;
即为所求;
试题解析:
解:(1)①补全图形如图所示;
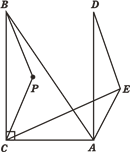
②如图,连接BD、CD,如图所示:
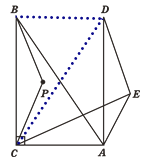
∵△BCP沿射线CA方向平移,得到△DAE,
∴BC∥AD且BC=AD,
∵∠ACB=90°,
∴四边形BCAD是矩形,
∴CD=AB=6,
∵BP=3,
∴DE=BP=3,
∵BP⊥CE,BP∥DE,
∴DE⊥CE,
∴在Rt△DCE中, ![]() ;
;
(2)证明:如图,当C、P、M、N四点共线时,PA+PB+PC最小
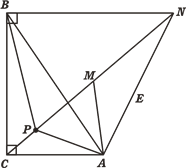
由旋转可得,△AMN≌△APB,
∴PB=MN
易得△APM、△ABN都是等边三角形,
∴PA=PM
∴PA+PB+PC=PM+MN+PC=CN,
∴BN=AB=6,∠BNA=60°,∠PAM=60°
∴∠CAN=∠CAB+∠BAN=60°+60°=120°,
∴∠CBN=90°
在Rt△ABC中,易得![]()
∴在Rt△BCN中, ![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x-y)(-y-x)的结果是( )
A. -x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.
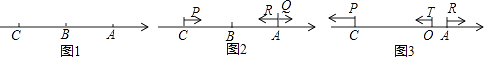
(1)若BC:AC=4:7,求点C到原点的距离;
(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT﹣MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x+3y)2-(3x+y)2的结果是( )
A. 8x2-8y2 B. 8y2-8x2 C. 8(x+y)2 D. 8(x-y)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=
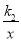 的图象交于A(一1,6)、B(a,一2)两点.
的图象交于A(一1,6)、B(a,一2)两点.(1)求一次函数的解析式;
(2)连接OA、0B,求ΔAOB的面积;
(3)当x满足_______________时, 0<y1≤y2.
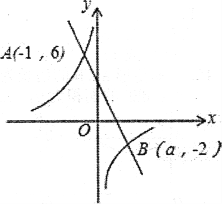
-
科目: 来源: 题型:
查看答案和解析>>【题目】数轴上A、B两点所对应的数分别是4和﹣6,则A、B两点间的距离为( )
A.﹣2
B.2
C.﹣10
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了掌握我市中考模拟数学考试卷的命题质量与难度系数,命题教师赴我市某地选取一个水平相当的初三年级进行调研,命题教师将随机抽取的部分学生成绩(得分为整数,满分为150分)分为5组:第一组75~90;第二组90~105;第三组105~120;第四组120~135;第五组135~150.统计后 得到如图所示的频数分布直方图(每组含最小值不含最大值)和扇形统计图.观察图形的信息,回答下列问题:
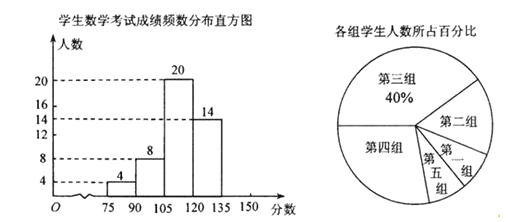
(1)本次调查共随机抽取了该年级 名学生,并将频数分布直方图补充完整:
(2)若将得分转化为等级,规定:得分低于 90分评为“D”,90~120 分评为“C”,120~135分评为“B”,135~150分评为“A”.那么该年级 1500名考生中,考试成绩评为“B”的学生有 名;
相关试题

