【题目】如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40. 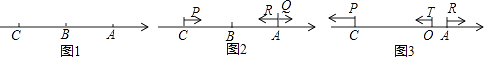
(1)若BC:AC=4:7,求点C到原点的距离;
(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问PT﹣MN的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
参考答案:
【答案】
(1)解:如图1,∵AB=60,BC:AC=4:7,
∴ ![]() =
= ![]() ,
,
解得:BC=80,
∵AB=60,点A对应的数是40,
∴B点对应的数字为:﹣20,
∴点C到原点的距离为:80﹣(﹣20)=100
![]()
(2)解:如图2,设R的速度为每秒x个单位,则
R对应的数为40﹣5x,
P对应的数为﹣100+15x,
Q对应的数为10x+15,
PQ=5x﹣115或115﹣5x
QR=15x﹣25
∵PQ=QR
∴5x﹣115=15x﹣25或115﹣5x=15x﹣25
解得:x=﹣9(不合题意,故舍去)或x=7
∴动点Q的速度是9个单位长度/秒.
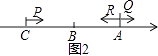
(3)解:如图3,设运动时间为t秒
P对应的数为﹣100﹣5t,T对应的数为﹣t,R对应的数为40+2t,
PT=100+4t,
M对应的数为﹣50﹣3t,N对应的数为20+t,
MN=70+4t
∴PT﹣MN=30,
∴PT﹣MN的值不会发生变化,是30.
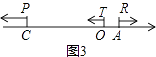
【解析】(1)根据AB=60,BC:AC=4:7,得出BC=80,利用点A对应的数是40,即可得出点C对应的数;(2)假设点R速度为x单位长度/秒,根据点P、Q之间的距离与点Q、R的距离相等,得出等式方程求出即可;(3)分别表示出PR,MN的值,进而求出PT﹣MN的值.
【考点精析】通过灵活运用数轴,掌握数轴是规定了原点、正方向、单位长度的一条直线即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,AABC的三个顶点坐标为A(一3,4),B(一4,2),C(一2,1),ΔABC绕原点顺时针旋转90°,得到△A1B1C1,ΔA1B1C1向左平移2个单位,再向下平移5个单位得到△A2B2C2.
(1)画出ΔA1B1Cl和△A2B2C2
(2)P(a,b)是AABC的AC边上一点,ΔABC经旋转、平移后点P的对应点分别为P1、P2,请写出点P1、P2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数有( ) ①已知直角三角形的面积为2,两直角边的比为1:2,则斜边长为
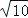 ;
;
②直角三角形的最大边长为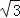 ,最短边长为1,则另一边长为
,最短边长为1,则另一边长为 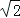 ;
;
③在△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC为直角三角形;
④等腰三角形面积为12,底边上的高为4,则腰长为5.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x-y)(-y-x)的结果是( )
A. -x2+y2 B. -x2-y2 C. x2-y2 D. x2+y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(x+3y)2-(3x+y)2的结果是( )
A. 8x2-8y2 B. 8y2-8x2 C. 8(x+y)2 D. 8(x-y)2
-
科目: 来源: 题型:
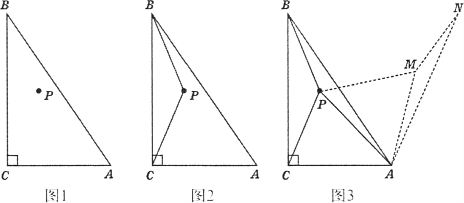
查看答案和解析>>【题目】如图1,在△ABC中,∠ACB=90°,点P为ΔABC内一点.
(1)连接PB,PC,将ABCP沿射线CA方向平移,得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将ΔABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系xoy中,一次函数y1=k1x+b的图象与反比例函数y2=
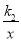 的图象交于A(一1,6)、B(a,一2)两点.
的图象交于A(一1,6)、B(a,一2)两点.(1)求一次函数的解析式;
(2)连接OA、0B,求ΔAOB的面积;
(3)当x满足_______________时, 0<y1≤y2.
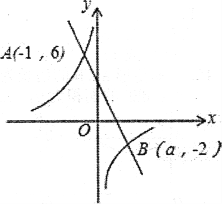
相关试题

